| by Jan Hakenberg, Ulrich Reif, Scott Schaefer, Joe Warren | published as viXra:1405.0012 – May 2nd, 2014 |
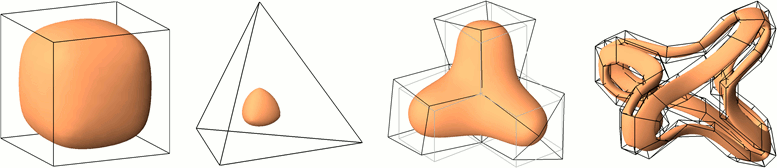
Figure:
Abstract: We present a framework to derive the coefficients of trilinear forms that compute the exact volume enclosed by subdivision surfaces. The coefficients depend only on the local mesh topology, such as the valence of a vertex, and the subdivision rules. The input to the trilinear form are the initial control points of the mesh.
Our framework allows us to explicitly state volume formulas for surfaces generated by the popular subdivision algorithms Doo-Sabin, Catmull-Clark, and Loop. The trilinear forms grow in complexity as the vertex valence increases. In practice, the explicit formulas are restricted to meshes with a certain maximum valence of a vertex.
The approach extends to higher order momentums such as the center of gravity, and the inertia of the volume enclosed by subdivision surfaces.
| Volume Enclosed by Subdivision Surfaces * |
|
980 kB |
| Volume Enclosed by Subdivision Surfaces (on viXra.org) |
|
link |
| On the Volume of Sets Bounded by Refinable Functions ** |
|
690 kB |
| On the Volume of Sets Bounded by Refinable Functions *** |
|
link |
The first author dedicates this work to the memory of Andrew Ladd, Nik Sperling, and Leif Dickmann. The first author was partially supported by personal savings accumulated during his visit to the Nanyang Technological University/Singapore as a visiting research scientist in 2012–2013. He'd like to thank everyone who worked to make this opportunity available to him.
Supplemental material:
| Examples for Doo-Sabin, Midedge, Catmull-Clark, and Loop |
|
link |
| Subdivision and Volume Implementation (Mathematica 9) |
|
2.4 MB |
| Alternating forms in numeric m-format (Matlab) |
|
360 kB |
The most punctual member of the household - Rocky, the German shepherd -
viewed Totto-Chan's unusual behavior with suspicion, but after a good stretch,
he positioned himself close to her, expecting something to happen.
from Totto-Chan
Presentation about the formula in practice:
[Peters/Nasri 1997] formulate an intuitive, iterative approximation of the volume:
At each iteration step the computational effort remains constant, while the value converges at an exponential rate.
At the time, they require "regular submeshes to have a polynomial parametrization" in order to derive the exact volume form for regular facets.
For instance, volumes defined by the Loop Butterfly-scheme were not covered by their approach.
Our new derivation allows to waive this constraint.
For the Butterfly-scheme we demonstrate the derivation in Example 7 of our preprint.
The approximation method by Peters/Nasri can now be used for a more general class of schemes. (Thanks to Jörg Peters for pointing this out to me.)
The approach by Bernd Schwald in his diploma Thesis Exakte Volumenberechnung von durch Doo-Sabin-Flächen begrenzten Körpern submitted in Stuttgart, 1999 already yields the exact volume enclosed by Doo-Sabin limit surfaces. The method evaluates infinite sums over the spline rings using a computer algebra system. There are restrictions on the subdivision weights. Neither infinite sums or restrictions on the weights occur in our new solution method.
The main finding of our publication is that the volume enclosed by subdivision surfaces is a trilinear form in the control points.
The volume enclosed by the surface defined by subdivision of a closed, orientable mesh M is of the form
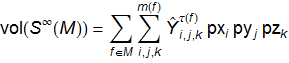
The surface is parameterized by a partition of facets. A facet f is typically a quad, or a triangle. The coefficients of the trilinear forms

are constant and only depend on the topology τ(f) of the facet f, for instance the valence of a non-regular vertex.
The coordinates in the neighborhood of facet f are enumerated as
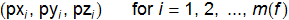
and completely define the subdivision surface associated to facet f.
We show that the trilinear forms are not uniquely determined. The solution space is a 3-dimensional vector space for all three subdivision schemes that we investigate. If we demand additionally that the trilinear forms be alternating, there is a unique solution. The collection of alternating trilinear forms is available for download.
Defeat doesn't finish a man, quit does.
A man is not finished when he's defeated.
He's finished when he quits.
Richard M. Nixon
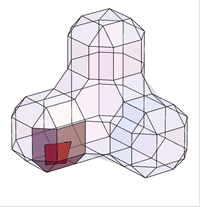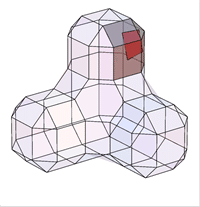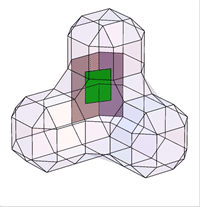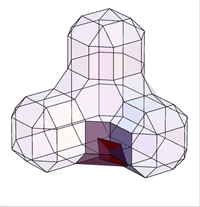
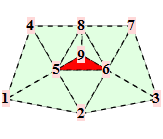
For a Doo-Sabin mesh, the points are from the 4 faces adjacent to each vertex of the mesh. The midpoints of the 4 faces span a quad. Common topololgies are
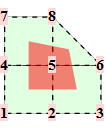

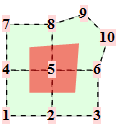
The corresponding trilinear forms have dimensions 8x8x8, 9x9x9, ... . At the moment, we have calculated the trilinear forms for valences up to 12. Some solutions are only in numeric precision.
| volume | centroid | inertia | |||||
|---|---|---|---|---|---|---|---|
| valence | # of coefficients | # unique ±,≠0 | solution | # unique ±,≠0 | solution | # unique ±,≠0 | solution |
| 3 | 8^3=512 | 30 | symbolic | 464 | symbolic | 1598 | symbolic |
| 4 | 9^3=729 | 13 | symbolic | 135 | symbolic | 378 | symbolic |
| 5 | 10^3=1000 | 63 | symbolic | ? | numeric | ||
| 6 | 11^3=1331 | 87 | symbolic | 1709 | symbolic | ||
| 7 | 12^3=1728 | ? | numeric | ? | numeric | ||
| 8 | 13^3=2197 | 147 | symbolic | ? | numeric | ||
| 9 | 14^3=2744 | ? | numeric | ? | numeric | ||
| 10 | 15^3=3375 | 221 | symbolic | ||||
| 11 | 16^3=4096 | ? | numeric | ||||
| 12 | 17^3=4913 | 313 | symbolic | ||||
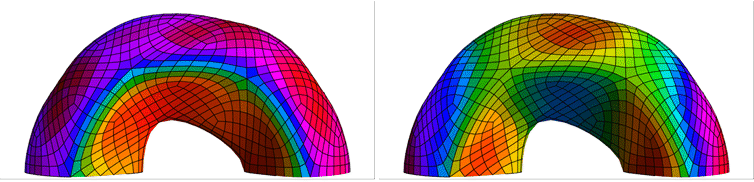
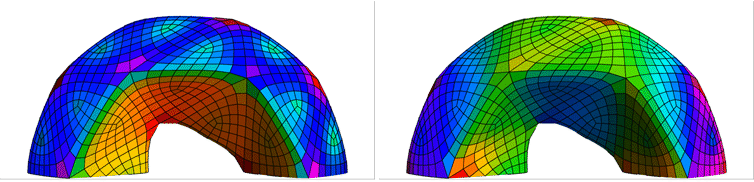
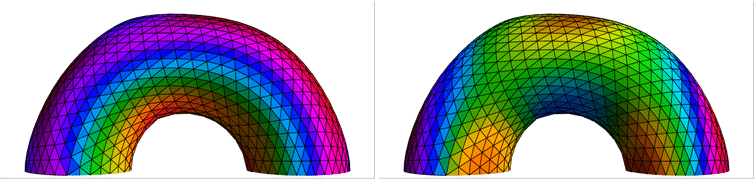
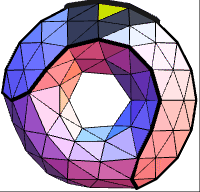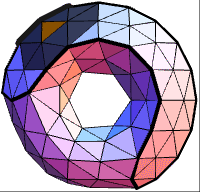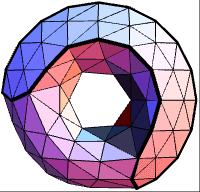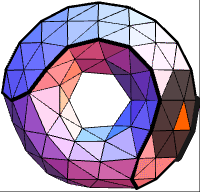
The contribution of each facet of a torus mesh to the global volume is color-coded.
Two iterations of the Midedge subdivision by [Peters/Reif 1997] in the simplest-pure specification is equivalent to Doo-Sabin with modified weights: [2 1 0 ... 0 1]/4 for all valences. For instance, to contract a point in a triangle, the mask is [2 1 1]/4. To contract a point of a quad, the weights are [2 1 0 1]/4, etc.
The weights are rational. The alternating forms are established in symbolic form up to valence 12. Since the scheme is used only rarely in practice, the forms are available on request.

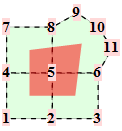
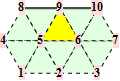
For a Catmull-Clark mesh the points are from the one-ring around a quad of the mesh. Common topololgies are
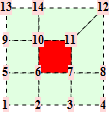
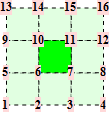
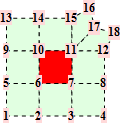
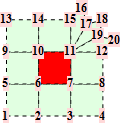

The corresponding trilinear forms have dimensions 14x14x14, 16x16x16, 18x18x18, ... . For valences up to 8, the straight forward approach is sufficient.
With the advanced formula presented in the preprint, we have calculated the trilinear forms for valences up to 16.
The mesh in the animation to the right is used as a showcase in our preprint. The initial control mesh consist of 4 unit cubes. The limit surface encloses an exact volume of
40180082442670051252900902177393516510211208965892170836569226629214212708997856639459 55070082910257403120169305663456114089964755513505550065666048314075696077889864924495 54641219821870336717316476247679551629672346929205592993625071348599372485886982248931 39701577318904153684167935446076618334003376802825747208498276611956468960741228369454 5858835385150366631268809254233132555169056767142562957502393768749712436004182071021 / 16046323710242313089909175392307959118108021410074742425376177351348347992382685285901 78569776586033890127193528209009943782818471786608583381312401834308895367788456365409 80388250356278333552494074499327159439890167562372988838107467187740355820288057315668 95736089226365074195187059803111007004229005368248251629007854376338913422782400877557 2142274115412160255773388520595334004563330096707755296887477615110463588476731392000 = 2.5040054761592054376437149098797625772569551310115694056260292100279...
For comparison, the approximation of the volume based on several rounds of subdivision, and evaluation of the volume of the piecewise linear surface is stated below:
3 -> 2.5205403043890737813... 4 -> 2.5081288596400819507... 5 -> 2.5050357452975922494... 6 -> 2.5042630141663386140...
The number of unique coefficients (up to sign) in the alternating form are approximately binomial(8+2v,3)/2. The divide by 2 is due to the mirror symmetry along the diagonal through the non-regular vertex of the facet.
| valence | # of coefficients | # unique ±,≠0 | solution |
|---|---|---|---|
| 3 | 14^3=2744 | 186 | symbolic |
| 4 | 16^3=4096 | 71 | symbolic |
| 5 | 18^3=5832 | 416 | symbolic |
| 6 | 20^3=8000 | 580 | symbolic |
| 7 | 22^3=10648 | 782 | symbolic |
| 8 | 24^3=13824 | 1026 | symbolic |
| 9 | 26^3=17576 | 1316 | symbolic |
| 10 | 28^3=21952 | 1656 | symbolic |
| 11 | 30^3=27000 | 2050 | symbolic |
| 12 | 32^3=32768 | 2502 | symbolic |
| 13 | 34^3=39304 | 3016 | symbolic |
| 14 | 36^3=46656 | 3596 | symbolic |
| 15 | 38^3=54872 | 4246 | symbolic |
| 16 | 40^3=64000 | 4970 | symbolic |
The contribution of each quad of a torus mesh to the global volume is color-coded.
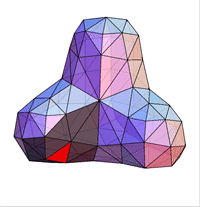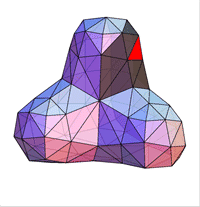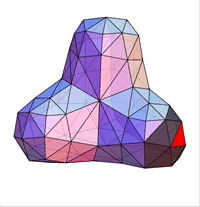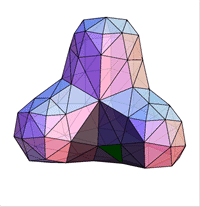
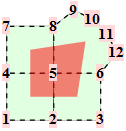
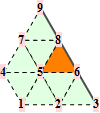
For a Loop mesh the points are from the one-ring around a triangular facet. Common topologies are
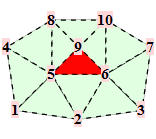


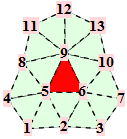
The corresponding trilinear forms have dimensions 9x9x9, 10x10x10, ... . At the moment, we have calculated the trilinear forms for valences up to 12. Some solutions are only in numeric precision.
| volume | centroid | ||||
|---|---|---|---|---|---|
| valence | # of coefficients | # unique ±,≠0 | solution | # unique ±,≠0 | solution |
| 3 | 9^3=729 | 46 | symbolic | 639 | symbolic |
| 4 | 10^3=1000 | 64 | symbolic | 1004 | symbolic |
| 5 | 11^3=1331 | 88 | symbolic | ? | numeric |
| 6 | 12^3=1728 | 43 | symbolic | 735 | symbolic |
| 7 | 13^3=2197 | ? | numeric | ? | numeric |
| 8 | 14^3=2744 | 188 | symbolic | ? | numeric |
| 9 | 15^3=3375 | ? | numeric | ||
| 10 | 16^3=4096 | ? | numeric | ||
| 11 | 17^3=4913 | ? | numeric | ||
| 12 | 18^3=5832 | ? | numeric | ||
The contribution of each triangle of a torus mesh to the global volume is color-coded.
Possible applications of our new formula are
Our framework makes it possible to obtain the trilinear forms that compute the volume enclosed by surfaces defined by three other well-known subdivision schemes:
Catmull-Clark and Loop subdivision allow B-spline curve subdivision along edge cycles. These edges are called crease edges. When the crease edges are sharp, i.e. the crease rule depth is infinite, new trilinear forms need to be derived in order to compute the enclosed volume. The surface near the sharp crease edges typically depends on fewer control points than for regular Catmull-Clark patches. Consequently, the trilinear forms have fewer coefficients. We treat sharp creases for Catmull-Clark and Loop in the next section.
The extension of our framework to moments of higher degree d is straightforward. Instead of trilinear forms, we have (d+3)-multilinear forms. This means however, that the number of coefficients grows steep in the degree of the momentum. Here is an overview for the regular topologies:
| scheme | center of gravity (d=1) | inertia (d=2) |
|---|---|---|
| Doo-Sabin | 9^4=6561 | 9^5=59049 |
| Catmull-Clark | 16^4=65536 | 16^5=1048576 |
| Loop | 12^4=20736 | 12^5=248832 |
Since these numbers put a preliminary end to our exploration in 3D, we fallback to the 2D case: subdivision of curves. We describe how to compute area, centroid, and inertia of the subset in the plane enclosed by a subdivision curve. The derivation and examples are published here.
The experience from the 2D case give us a new perspective on the moments in 3D. By accounting for symmetries in the tensor coefficients, we are able to obtain the forms for the surface case after all. The approach and results are summarized here.
I have always tried to live in an ivory tower,
but a tide of shit is beating at its walls,
threatening to undermine it.
Gustave Flaubert
| by Jan Hakenberg, Ulrich Reif, Scott Schaefer, Joe Warren | published as viXra:1406.0060 – June 10th, 2014 |

Figure:
Abstract: Subdivision surfaces with sharp creases are used in surface modeling and animation. The framework that derives the volume formula for classic surface subdivision also applies to the crease rules. After a general overview, we turn to the popular Catmull-Clark, and Loop algorithms with sharp creases. We enumerate common topology types of facets adjacent to a crease. We derive the trilinear forms that determine their contribution to the global volume. The mappings grow in complexity as the vertex valence increases. In practice, the explicit formulas are restricted to meshes with a certain maximum valence of a vertex.
| Volume Enclosed by Subdivision Surfaces w/ Sharp Creases |
|
* 630 kB |
| Volume Enclosed by Subdivision Surfaces w/ Sharp Creases |
|
link |
| Examples for Catmull-Clark, and Loop w/ Sharp Creases |
|
link |
| Subdivision and Volume Implementation (Mathematica 9) |
|
2.4 MB |
Presentation about the formula in practice:
Surface subdivision schemes are tuned to produce surfaces that appear smooth everywhere. Creases are a simple extension that provide the option to model sharp features in the surface. Across the crease, the surface normal is generally not continuous, as can be seen in the illustration above.
In Piecewise smooth surface reconstruction Hoppe et al., 1994, extend the Loop subdivision scheme to handle sharp creases. In Subdivision Surfaces in Character Animation DeRose et al., 1998, present refinement of creases in Catmull-Clark meshes. The concept is the same in both algorithms: Along an edge cycle of the mesh that is designated as crease, cubic B-spline subdivision rules for curves apply. In particular, control points that are not part of the crease cycle do not affect the refinement of the crease. In the limit, the crease is identical to a cubic B-spline curve.
An early use of sharp creases in subdivision surfaces was to model the fingernails of the character Geri in Pixar's 1997 short film Geri's game. From then on, subdivision with creases has been a tool in surface modeling, and frequently used in animations, as explained in the video by Autodesk.
Die Laster stritten, wer von ihnen
am eifrigsten gewesen sei,
dem Bösen auf der Welt zu dienen;
den Preis erhielt die Heuchelei.
Johann Wilhelm Ludwig Gleim
The Catmull-Clark subdivision scheme was published in 1978. The Loop scheme was introduced 1987.
One round of cubic B-spline subdivision for curves consists of vertex repositioning, and mid-edge vertex insertion. The subdivision rules along crease edge cycles in a mesh are illustrated in the following.
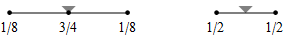
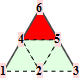
When f is adjacent to a crease, we denote the topology type by a tuple n.m. The first number n is the valence of the non-regular vertex (that also belongs to the crease). The second number m enumerates different configurations of the crease. All topology types are illustrated graphically. The subdivision weights are integer fractions. That means we can establish the trilinear forms in exact, symbolical notation. However, as the valence of the non-regular crease vertex increases, the volume forms become more difficult to establish because of computer memory constraints.


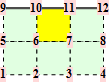
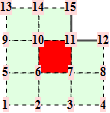

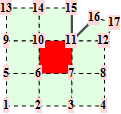


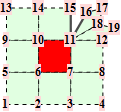
For the reader's convenience, we calculate the trilinear forms for crease facets with valences up to 5.
| topology | # of coefficients | # unique ±,≠0 | solution |
|---|---|---|---|
| 1.1 | 9^3=729 | 45 | symbolic |
| 2.1 | 12^3=1728 | 102 | symbolic |
| 3.1 | 15^3=3375 | 232 | symbolic |
| 3.2 | 14^3=2744 | 359 | symbolic |
| 4.1 | 17^3=4913 | 660 | symbolic |
| 4.2 | 16^3=4096 | 555 | symbolic |
| 5.1 | 19^3=6859 | 492 | symbolic |
| 5.2 | 19^3=6859 | 949 | symbolic |
| 5.3 | 18^3=5832 | 811 | symbolic |

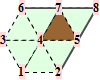
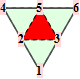

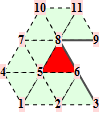
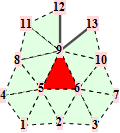
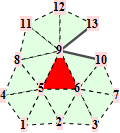
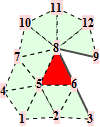
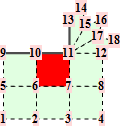
For the reader's convenience, we calculate the trilinear forms for crease facets with valences up to 6.
| volume | centroid | ||||
|---|---|---|---|---|---|
| topology | # of coefficients | # unique ±,≠0 | solution | # unique ±,≠0 | solution |
| 1.1 | 8^3=512 | 31 | symbolic | 387 | symbolic |
| 1.2 | 6^3=216 | 11 | symbolic | 104 | symbolic |
| 1.3 | 6^3=216 | 6 | symbolic | 40 | symbolic |
| 2.1 | 8^3=512 | 56 | symbolic | 756 | symbolic |
| 3.1 | 10^3=1000 | 64 | symbolic | 1002 | symbolic |
| 3.2 | 9^3=729 | 43 | symbolic | 631 | symbolic |
| 4.1 | 11^3=1331 | 161 | symbolic | 2928 | symbolic |
| 4.2 | 10^3=1000 | 120 | symbolic | 1980 | symbolic |
| 5.1 | 12^3=1728 | 115 | symbolic | ||
| 5.2 | 12^3=1728 | 216 | symbolic | ||
| 5.3 | 11^3=1331 | 165 | symbolic | ||
| 6.1 | 13^3=2197 | 282 | symbolic | ||
| 6.2 | 13^3=2197 | 282 | symbolic | ||
| 6.3 | 12^3=1728 | 220 | symbolic | ||
A teacher affects eternity: he can never tell where his influence stops. Henry Adams
We have derived the alternating trilinear forms for facets adjacent to sharp creases that are required to compute the volume enclosed by the subdivision surface. The forms are available up to a certain valence of the non-regular vertex. In the future, trilinear forms for greater valences may be computed.
The discussion in our article is restricted to meshes with pairwise disjoint crease cycles. [Hoppe et al. 1994] incorporates two other possibilities:
The contribution to the volume by a facet adjacent to a dart, or corner vertex is determined by yet other trilinear forms. The forms depend on the valence of the vertex and require an enumeration alike the one carried out in the previous chapter.
The great recurring themes of human history,
the balance between cooperation and conflict.
Matt Ridley
The first author was traveling in Vietnam during the time of this project. Here are photos of hotel rooms with spacious desks to place a laptop on. At the time, he was not affiliated to any academic institution.
Personal note from Jan: I was surprised to find that one needs endorsement to post on arXiv. Also, arXiv has many different categories, and selecting the right category for this work seems the hardest feat of all. So, I decided that viXra suits me better.