On Moments of Sets Bounded by Subdivision Surfaces

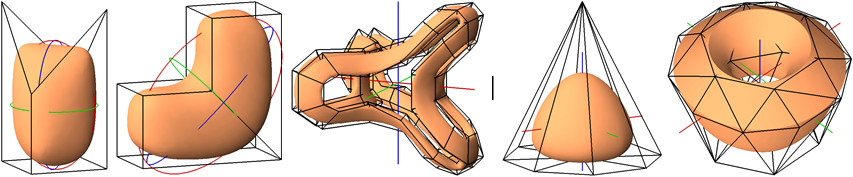
Figure: Doo-Sabin: The unit cube with two opposite corners elevated by 1 defines a subdivision surface that encloses a set with centroid

For a set bounded by a limit surface corresponding to a control mesh with vertices of valence 3, and 4 we compute the ellipsoid with equivalent inertia. | Loop: The centroid defined by the subdivision surface is at the intersection of the red, green, and blue lines. The surface right features sharp creases.

Abstract: The volume enclosed by subdivision surfaces, such as Doo-Sabin, Catmull-Clark, and Loop has recently been derived. Moments of higher degree d are more challenging because of the growing number of coefficients in the (d+3)-linear forms. We derive the intrinsic symmetries of the tensors, and thereby reduce the complexity of the problem formulation.

Our framework allows to compute the 4-linear forms that determine the centroid defined by Doo-Sabin, and Loop surfaces, including Loop with sharp creases. For Doo-Sabin surfaces, we also establish the tensors of rank 5 that determine the inertia for valences 3, and 4. When the subdivision weights are rational, the centroid, and inertia are obtained as exact, symbolic values. In practice, the formulas are restricted to meshes with a certain maximum valence of a vertex.

On Moments of Sets Bounded by Subdivision Surfaces *	on_moments...pdf	790 kB
On Moments of Sets Bounded by Subdivision Surfaces	viXra:1408.0070	link
Centroid & Inertia defined by Example Subdivision Surfaces	viXra:1409.0026	link
Subdivision and Moments Implementation (Mathematica 9)	moments_surf...zip	180 kB

* latest edition, modified last on September 5th, 2014

The first author dedicates this work to the memory of Andrew Ladd, Nik Sperling, and Leif Dickmann. The first author was partially supported by personal savings accumulated during his visit to the Nanyang Technological University/Singapore as a visiting research scientist in 2012–2013. He'd like to thank everyone who worked to make this opportunity available to him.

Oh please don't.
I 'm finished,
and glad of it.
V

The moments derived in the article have diverse applications:

• The formulas allow to design subdivision surfaces with exact volume, centroid, and inertia.
• By translation of control points, surfaces can be deformed subject to preservation of moments.
• Countless computer games and animations use subdivision surfaces for character and shape modeling. If a subdivision surface is the contour of an animated entity, our formulas help to make the motion more accurate: Unaccelerated rotation is around the centroid; the inertia determines the preservation of angular momentum.
• [Prevost et al. 2013] and [Baecher et al. 2014] explain the significance of the centroid and inertia in the context of 3d printing.

A simple formula for the moment of the set bounded by the limit surface was not known previously. [Peters/Nasri 1997] only describe an approximation of the moment. Moreover, their framework requires "regular submeshes to have a polynomial parametrization". Moments defined by the Loop scheme are not covered by their approach.

[Gonzalez et al. 1998] carry out the derivation of moments of sets bounded by piecewise polynomial surfaces. Their derivation is sufficient for surfaces that are entirely constructed from B-spline, or Bézier/Bernstein patches, for instance.

This article completes our trilogy in four parts.

• 
  x
• 
  y
• 
  z
• 
  xx
• 
  yy
• 
  zz
• 
  xy
• 
  yz
• 
  zx

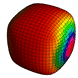
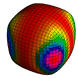
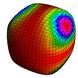
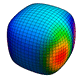
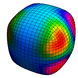
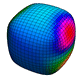
Figure: The unit-cube is subdivided several rounds with Doo-Sabin's algorithm. The facets of the dual mesh are colored based on their contribution to the moment of the monomial indicated.

Future work

• All our examples were computed on a computer with 8 GB memory. In particular, forms for the centroid computation of Catmull-Clark surfaces are not established yet. With a more powerful machine, tensors for schemes with larger support than Doo-Sabin and Loop and higher valence vertices can be computed.
• The number of unique coefficients up to sign is still slightly lower than the assumed number of variables. Extra effort could be taken to identify non-trivial symmetries to further reduce the size of the linear system.

Remark

In December 2016, we have devised a tensor iteration to find approximate answers to some of the remaining questions.

Mozart tells us what it's like to be human,
Beethoven tells us what it's like to be Beethoven,
and Bach tells us what it's like to be the universe.
Douglas Adams