Iterative Computation of Moment Forms for Subdivision Surfaces

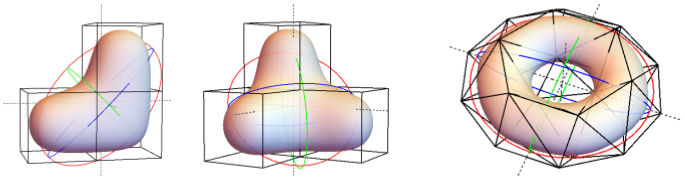
Figure: Solids bounded by Catmull-Clark and Loop subdivision surfaces with centroids indicated by dashed lines, and inertia indicated by the principal axes of the ellipsoid with equivalent inertia. The iterative derivation of multilinear forms determines the moments with unprecedented accuracy.

Abstract: The derivation of multilinear forms used to compute the moments of sets bounded by subdivision surfaces requires solving a number of systems of linear equations. As the support of the subdivision mask or the degree of the moment grows, the corresponding linear system becomes intractable to construct, let alone to solve by Gaussian elimination. In the paper, we argue that the power iteration and the geometric series are feasible methods to approximate the multilinear forms. The tensor iterations investigated in this work are shown to converge at favorable rates, achieve arbitrary numerical accuracy, and have a small memory footprint. In particular, our approach makes it possible to compute the volume, centroid, and inertia of spatial domains bounded by Catmull-Clark and Loop subdivision surfaces.

Our framework allows to compute the 4- and 5-linear forms that determine the centroid and inertia defined by Doo-Sabin, Loop, and Catmull-Clark subdivision surfaces up to arbitrary precision.

The approach is analogous to the one-time computation of an approximation of pi=3.14159265... Once the value of pi is fixed, for instance on a chip of a pocket calculator, the well-known formulas yield the approximate circumference and area of a circle of arbitrary radius.

Iterative Computation of Moment Forms	iterative_com....pdf	590 kB
Iterative Computation of Moment Forms (on viXra.org)	viXra:1703.0267	link
Iterative Computation of Moment Forms (Mathematica 10.3)	..._moments_3d.zip	160 kB
Moment forms for Subdivision Curves (Mathematica 10.3)	..._moments_2d.zip	70 kB

The first author dedicates this work to the memory of Elvisa Herr, Andrew Ladd, Nik Sperling, and Leif Dickmann. The first author was partially supported by personal savings accumulated during his employment with Nutonomy/Asia as a software architect in 2015–2016. He'd like to thank everyone who worked to make this opportunity available to him.

Willst Du Dich am Ganzen erquicken,
so mußt Du das Ganze im Kleinen erblicken.
Johann Wolfgang von Goethe

Characteristics of Approach

The iteration methods do not require to build the huge system matrix, or solve a linear system. Instead, the storage of the form coefficients as a vector is sufficient. The vector of coefficients is subject to a linear transformation that is computed in place, i.e. without building the corresponding matrix. The vector transformation is repeated iteratively. Each iteration step enhances the accuracy of the form. In the limit, the vector contains the exact coefficients of the moment form.

Our work introduces two exploits:

• obtain the solution to a linear system via iteration (instead of using a solver)
• the linear transformations of the coefficient vector is computed directly on the vector elements instead of building the matrix

The iterations that provide the solution to the linear system are of two types:

• The forms for the inhomogeneous system, i.e. for non-regular patches, can be computed using a finite geometric series.
• The forms for the homogeneous system, i.e. for regular patches, can be computed using the power iteration, also known as Von Mises iteration.

Both exploits and iteration methods play an essential role when computing moment forms for previously unobtainable cases:

• Catmull-Clark centroid and intertia forms for valences 3, 5, 6, 7, 8 using the geometric series
• Butterfly centroid form for regular case using the power-iteration by von-Mises

Geld ist wertlos,
verglichen mit der Freizeit.
Cro

The video is an overview to the introduced tensor iterations for the one-time computation of moment forms.

Be humble to go further.
Vietnamese saying

Eigenvalues of Homogeneous System

The requirements for the convergence of the geometric series is simple to confirm via the eigenvalues of the relatively small subdivision matrix.

Of greater interest are the eigenvalues of the homogeneous system that is subject to the power-iteration by von-Mises. Below, we tabulate the eigenvalues and their multiplicity of the homogeneous system for the most common surface schemes.

We build the matrices for the purpose of analysis only. When performing the von-Mises iteration, the construction of the matrices is not required.

The symmetries of the moment form are exploited in order to reduce the number of coefficients. Symmetries that stem from the tensor product structure of the basis functions in case of Doo-Sabin and Catmull-Clark are not considered.

Doo-Sabin

Loop

Catmull-Clark

Butterfly with w=1/16

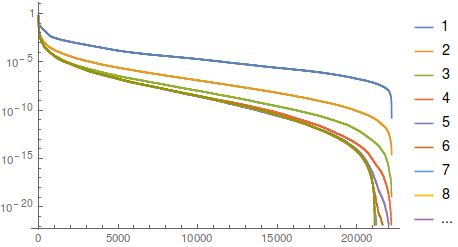
The Butterfly centroid form for the regular patch is computed using the power-iteration method. The graphic below shows the 22194 tensor entries in each step of the iteration sorted by magnitude.

Two's company,
three's a crowd.

Remarks

In practise, we have used the power-iteration by von-Mises in a single application only: to establish the coefficients of the centroid form for the Butterfly regular case.

Alternative methods are typically preferable:

• The basis-functions for the regular Doo-Sabin and Catmull-Clark refinement are polynomials. Symbolic intergration was used to obtain the exact coefficients of the moment forms.
• For the refinement of regular Loop and Butterfly patches the exact symbolic nullspace vectors of the homogeneous system minus the identity matrix was established.
• For common curve subdivision schemes the low number of form coefficients permits the computation via the nullspace.

Good judgement is the result of experience.
Experience is the result of bad judgement.
Fred Brooks