Jaya was developped to perform smooth freeform deformation on 3d-models. Soon it became a tool, to build volumetric models, from which surfaces can be exported to serve as the conventional representation of an object in the computer. The code deals with triangles, tetrahedra, octahedra.
Then, there was another extention to Jaya: Rigid skeletons are used to fix several control points of the volumetric coarse control mesh while deforming. Other control points can move freely and are used, for instance, to compensate volume loss in the neighborhood of a joint of the skeleton. Main goal was to deliver a tool which automizes the creation of animations of 3d surface models.
| Smooth Subdivision of Tetrahedral Meshes * |
|
2.6 MB |
| SourceCode (C++ using openGL & GHOST) ** |
| 3.4 MB |
The paper Barycentric coordinates for convex sets is a good reference to learn the math behind freeform-deformation. To deform a given triangular model, such as the dinosaur, one lays out a coarse volumetric control mesh. The control mesh needs to cover the parts of the model that are to be deformed, for instance the extremities of the dinosaur. After several rounds of volumetric subdivision on the control mesh, the model should still be contained by the subdivided mesh. At this state, we detect which model vertices is contained by which volumetic cell. Each model vertex is stored in baricentric coordinates with respect to the volumetric cell. After a repositioning (deformation) of the control mesh, the subdivided volumetric cells deform too. With the baricentric coordinates at hand, each model vertex can be updated with the original baricentric coordinates of the deformed volume cell. This process is essentially a sparse matrix multiplication, hence a hash table should be used for real-time needs.
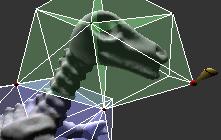

The brush is used to lay out the control mesh. I.e. we create basic shapes (tetrahedra, etc.) and repositioning vertices of the existing mesh. A special feature is, that draging on a triangle belonging to an existing shape, creates a new tetrahedra on top of that triangle. This allows fast and convenient construction! Forcefeedback comes into play, for easier navigation: control mesh vertices attract the phantom if close enough.
The hand has selective character. In order to be able to apply transformations only locally, i.e. only on a subset of the control mesh, we use coloring, to indicate different contextural regions, such as the head and the arms of the dinosaur. Furthermore, we can associate options to vertices. Namely, that it could be restricted to the yz-plane, or has a partner vertex mirrored across the yz-plane, which will move the pair simultaneously. We also can protect vertices from being moved at all (they appear red).
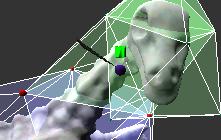
The feather moves all vertices, that touch the contextural region, that matches the current selected color. In the picture we apply an affine traformation to the green region of the control mesh, that coveres the head. The transformation is defined by Inverse[PhantomMatrix at button down time]*(current PhantomMatrix). The average normals of the surface of the model are updated as soon as the transformation is complete.
Ich habe die Erfahrung gemacht,
dass Leute ohne Laster
auch sehr wenige Tugenden haben.
Abraham Lincoln
The dinosaur sculpture scanned by Cyberware.
At one point, we associate each model vertex v with the cell of the subdivided volumetric mesh, that containts v. To do this efficiently, we sort both the vertices and the cells accorting to their z-coordinate (could be x or y respectively) in the bottom-up fashion. For each vol cell we collect into a second set the vertex with the lowest z coordinate. Now we can make an interwinded loop thru the two datasets.
Using axis aligned bounded box check for vertices, that are on the same z level as volumetric cells, selects those model vertices, for which we do the rather expensive baricentric coordinate computation. If all baricentric coordinates are > 0, the vertex can be assigned to the current volume cell.
Our implementation requires 7 sec to perform on 28098 model vertices vs. 23588 vol. cells (the dinosaur example with 4 rounds of subdivision). The code is given below, sorting (QuickSort) is done in the array library.
void baryModelQS(void) {//standalone optimized modelV->subdivBary
int c1,c2,c3,c4,csh,cnt=0,n,id,f,env,ind[5],nV=mact->size[1],nS=0;
int btic=clock();
char canBe=0;
float n1,nj,nk,sum,vol;
int lb=subdiv->getVertex(0)->length-4; //# of control points
Face fa;
printf("baricentric:");
if (mbar) delete mbar; //mbar is a [cP x mV]
mbar=new matrix<float>(lb,nV,"");
matrix<float> v(3,1,"");
for (c1=0;c1<subdiv->getNumFaces();c1++) //cnt number of volume shapes
if (subdiv->getFace(c1)->length>3) nS++;
array<float> mvsy(1,&nV,0); //sort model vert
for (c1=0;c1<nV;c1++) {
mvsy.data[c1]=mact->data[10*c1+8]; //before: [4*c1+1]
mbol->data[c1]=false; }
array<int> mvsi=mvsy.sort();
array<float> sinx(1,&nS,0),saxx(1,&nS,0),sinz(1,&nS,0),saxz(1,&nS,0); //bnd box
array<float> siny(1,&nS,0); //det lower and upper bnd
array<float> saxy(1,&nS,0);
cnt=0;
for (c1=0;c1<subdiv->getNumFaces();c1++) //cnt number of volume shapes
if ((env=subdiv->getFace(c1)->length)>3) {
saxx.data[cnt]=sinx.data[cnt]=subdiv->getVertex(subdiv->getFace(c1)->data[0])->data[0];
saxy.data[cnt]=siny.data[cnt]=subdiv->getVertex(subdiv->getFace(c1)->data[0])->data[1];
saxz.data[cnt]=sinz.data[cnt]=subdiv->getVertex(subdiv->getFace(c1)->data[0])->data[2];
for (c2=1;c2<env;c2++) {
n1=subdiv->getVertex(subdiv->getFace(c1)->data[c2])->data[0];
sinx.data[cnt]=MIN(sinx.data[cnt],n1);
saxx.data[cnt]=MAX(saxx.data[cnt],n1);
n1=subdiv->getVertex(subdiv->getFace(c1)->data[c2])->data[1];
siny.data[cnt]=MIN(siny.data[cnt],n1);
saxy.data[cnt]=MAX(saxy.data[cnt],n1);
n1=subdiv->getVertex(subdiv->getFace(c1)->data[c2])->data[2];
sinz.data[cnt]=MIN(sinz.data[cnt],n1);
saxz.data[cnt]=MAX(saxz.data[cnt],n1);
}
cnt++;
}
array<int> sisi=siny.sort();
printf(" AABB/QS. S:%i V:%i\n",nS,nV);
int cs=0,cv=0;
while (cs<nS&&cv<nV) {
if (saxy.data[sisi.data[cs]]<mvsy.data[cv]) cs++; else
if (siny.data[cs] >mvsy.data[cv]) cv++; else
{
csh=sisi.data[cs];
printf("\r %i - %i",cs,cv);
fa=*subdiv->getFace(csh);
matrix<float> shape=face2shape(subdiv,csh);
n=shape.size[1];
id=shapeid(shape);
f=bvfn[id]->size[1]; //# of faces
env=bfv[id]->size[0]; //# faces around each vertex
matrix<float> col(lb,fa.length,""); //holds bary coords for all verts of fa
for (c2=0;c2<fa.length;c2++)
memcpy(col[lb*c2],&subdiv->getVertex(fa.data[c2])->data[4],4*lb);
matrix<float> w(n,1,"");
matrix<float> *N=new matrix<float>[f]; //array of matrices
for (c1=0;c1<f;c1++) N[c1]=normal(shape,c1);
c1=0;
while (saxy.data[csh]>mvsy.data[cv+c1]) {//for cs check v's
c2=mvsi.data[cv+c1]; //hard adress of current model vertex
if (!mbol->data[c2])
if (sinx.data[csh]<mact->data[c2*10+7]&&mact->data[c2*10+7]<saxx.data[csh]) //before: [+0 +0
if (sinz.data[csh]<mact->data[c2*10+9]&&mact->data[c2*10+9]<saxz.data[csh]) // +2 +2
{
sum=0; canBe=1;
for (c3=0;c3<n;c3++) {//loop over the shape vertices and assign weight!
w.data[c3]=0;
v.data[0]=shape.data[c3*shape.size[0] ]-mact->data[c2*10+7];
v.data[1]=shape.data[c3*shape.size[0]+1]-mact->data[c2*10+8];
v.data[2]=shape.data[c3*shape.size[0]+2]-mact->data[c2*10+9];
memcpy(ind,&bfv[id]->data[env*c3],4*env); //outside
n1=v|N[ind[0]];
for (c4=1;c4<env-1;c4++) {//for^4 sad and rare occasion
vol=fabs(N[ind[0]]|N[ind[c4]]&N[ind[c4+1]]); //can be comp outside
nj=v|N[ind[c4]];
nk=v|N[ind[c4+1]];
w.data[c3]+=vol/(n1*nj*nk);
}
if (w.data[c3]<0) {canBe=0; break;}
sum+=w.data[c3];
}
if (canBe) {//comp real barys then
mbol->data[c2]=true;
w*=(1/sum);
memcpy((*mbar)[lb*c2],(col*w).data,4*lb);
}
}
c1++;
if (cv+c1>=nV) break;
} //eo loop over all Vertices
delete[] N;
cs++;
}
}
printf(" %5.2f sec ",(clock()-btic)*.001);
cnt=0;
for (c1=0;c1<nV;c1++) if (!mbol->data[c1]) cnt++;
printf(" (%i not allocated)\n",cnt);
}
It is by logic we solve,
but it is by intuition we create.
Pranav Mistry