Computer Graphics

Above, raytraced pics with Deian Tabakov. Unfortunately, the code is lost. I made a new raytracer.

Interactive World Simulation

Wave Particles et cetera

Color3D

Jaya · 3D Modeling and Deformation

Texture Advection for Fluid Flow

Single Image Stereogram

Edge-Aware Filtering

Even more ancient: Fractals in PowerBASIC.

The woods are lovely, dark, and deep,
But I have promises to keep,
And miles to go before I sleep,
And miles to go before I sleep.
Robert Frost

Single Image Stereogram

scene

depth

stereogram (click to enlarge)

The algorithm is adapted from Real-Time Stereograms of the book 'GPU Gems'.

function bmp=stereogram(depth)
% creates greyscale single-image-stereogram of depth field
%  depth     (n,m)-matrix
% which has values in the interval [0,1]
% please scale depth so that an entry with value
%  0 is farthest
%  1 is closest
% the algorithm works best if
%  m ranges between 480 and 1280
    
ofs=80;
sca=16;

bmp=repmat(uint8(rand(size(depth)+[0 ofs])*255),[1 1 3]);
for cy=1:size(depth,1)
  acc=0;
  for cx=1:size(depth,2)        
    inc=depth(cy,cx)*sca+acc;
    res=floor(inc);
    acc=inc-res;
    bmp(cy,ofs+cx,:)=bmp(cy,cx+res,:);
  end
end    
bmp(:,1:ofs,:)=[];
imshow(bmp)

The use of random noise texture is suitable for animations (hope for loss-less compression)...

If you have a problem,
and you can't solve it alone,
evoke it.
African proverb

Edge-Aware Filtering

face

flower

puzzle

castle

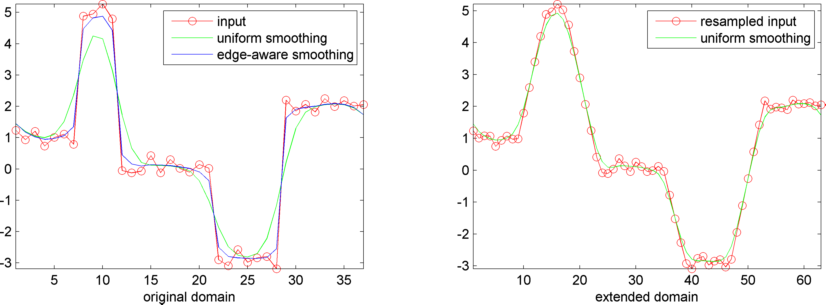
Eduardo Gastal and Manuel Oliveira have introduced a simple and efficient algorithm to carry out edge-aware image transformations, for instance edge-preserving smoothing. Their method Domain Transform for Edge-Aware Image and Video Processing was published at Siggraph 2011.

Douglas R. Lanman shares source code on Bilateral Filtering. The package also contains a nice cartoon renderer. I have replaced his implementation of the edge-preserving filter with the new, faster algorithm, to speed up the cartoon renderering.

Edge-Aware Filtering (Matlab) *

edgeaware.zip

270 kB

cartoon.m by Douglas R. Lanman, colorspace.m by Pascal Getreuer.

Below is the 40 lines listing of my implementation in Matlab. The emphasis is on simplicity and compactness:

function img=edgeawared(img) % img has double values between 0 and 1

for wid=[3 1]; % support of filter
  for c1=1:size(img,1)
    dom=ji1domain(img(c1,:,:));
    for c3=1:size(img,3)
      img(c1,:,c3)=ji1edgeaware(wid,img(c1,:,c3),dom);
    end
  end
  for c1=1:size(img,2)   
    dom=ji1domain(img(:,c1,:));
    for c3=1:size(img,3)
      img(:,c1,c3)=ji1edgeaware(wid,img(:,c1,c3)',dom)';
    end
  end
end  

function dom=ji1domain(sig)
  sz=size(sig);
  sz(find(sz==1))=[]; 
  sig=reshape(sig,sz)';
  dom=cumsum(1+sum(abs([zeros(sz(2),1) diff(sig,1,2)]),1));

function res=ji1edgeaware(w,sig,dom)
  if nargin==2
    dom=cumsum(1+[0 abs(diff(sig))]);
  end
  dom(end)=ceil(dom(end)); % small error happens here
  smp=1:dom(end);
  itr=interp1(dom,sig,smp);  
  res=interp1(smp,ji1filter(w,itr),dom);

function res=ji1filter(w,sig)
  w=2*w+1;
  x=linspace(-2,2,w);        
  fil=sqrt(1/pi)*exp(-x.*x); 
  fil=fil/sum(fil);          
  num=numel(sig);
  f_sig=fft(sig);
  f_fil=fft(fil,num);  
  res=ifft(f_sig.*f_fil);
  res=real(res);    
  res=res([(w+1)/2:end 1:(w-1)/2]);

The figure below illustrates how the algorithm operates on a 1-dimensional domain. The signal is warped onto a streched domain and resampled uniformly. This allows to apply a standard gaussion smoothing filter. Inverting the warp and resampling over the original domain yields the smoothed signal with edges preserved.

The extraordinary is in what we do,
not who we are.
Lara Croft