Fractals in PowerBASIC

This page contains PowerBASIC 2.1 programs, which generate fractals. The content was part of my first homepage. Since I had difficulties in gathering the sources, I want to contribute them yet.

Sierpinski

FOR X=0 TO 2^6-1
 FOR Y=0 TO 2^6-1-X
  IF (X AND Y) = 0 THEN PSET (X,Y)
 NEXT Y
NEXT X

Starwars

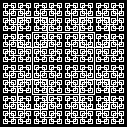
BOX 320,240,2^5-1
SUB BOX (X,Y,R)
 IF INT(R) <> 0 THEN
  BOX X+R,Y-R,R/2
  BOX X-R,Y-R,R/2
  BOX X+R,Y+R,R/2
  BOX X-R,Y+R,R/2
  LINE (X-R,Y-R)-(X+R,Y+R),,B
 END IF
END SUB

Root

PSET (320,0)
LIN 320,0,32
SUB LIN (X,Y,R)
 IF INT(R) > 0 THEN
  LINE -(X,Y)
  LIN X+R,Y+R,R/2
  PSET (X,Y)
  LIN X-R,Y+R,R/2
 END IF
END SUB

Snowflake

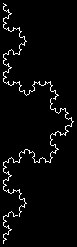
SHARED pi,x,y,a : pi=3.141592654
PSET (x,y)
STAR 4
SUB STAR (l?)
 IF l? > 0 THEN
  DRW 0       : STAR l?-1
  DRW pi/3    : STAR l?-1
  DRW -pi*2/3 : STAR l?-1
  DRW pi/3    : STAR l?-1
 END IF
END SUB
SUB drw (aq)
 IF aq THEN
  INCR a,aq
  INCR x,COS(a)*3
  INCR y,SIN(a)*3
  LINE -(x,y)
 END IF
END SUB

Mandelbrot

FOR I=-1.3 TO 1.3 STEP .01
 FOR R=-2.2 TO 1   STEP .01
  c=0 : b=0 : a=0 : count%=0
  WHILE ABS(a)<=2 AND ABS(b)<=2 AND count%<128
   c=a*a-b*b+R
   b=2*a*b+I
   a=c
   INCR count%
  WEND
  PSET (230+R*100,140+I*100),count%
 NEXT R
NEXT I

Weitere Iterationsformeln für z^3, z^4, z^5 jeweils +(r,i):

   a2=a*a
   b2=b*b
   c=a2*a-3*a*b2+r
   b=3*b*a2-b2*b+i
   a=c
   
   a2=a*a
   b2=b*b
   ab=a*b
   c=a2*a2-6*a2*b2+b2*b2+r
   b=4*(a2*ab-b2*ab)+i
   a=c
   
   a2=a*a
   b2=b*b
   a3=a2*a
   b3=b2*b
   c=a2*a3-10*a3*b2+5*b2*b2*a+r
   b=5*a2*a2*b-10*b3*a2+b2*b3+i
   a=c

Julia

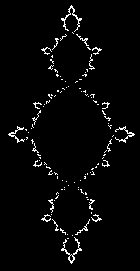
xc=-1  : yc=0
xn=.25 : yn=0
FOR i=1 to 10000
 a=xn-xc : b=yn-yc
 IF a>0 THEN
  xn=SQR((SQR(a*a+b*b)+a)/2)
  yn=b/(2*xn)
 ELSE
  IF a<0 THEN yn=SQR((SQR(a*a+b*b)-a)/2)
  IF b<0 THEN yn=-yn : xn=b/(2*yn) ELSE xn=SQR(ABS(b)/2)
  IF xn>0 THEN yn=b/(2*xn) ELSE yn=0
 END IF
END IF
IF i=1 THEN INCR xn,.5
IF RND>.5 THEN xn=-xn : yn=-yn
PSET (160+xn*80,100-yn*80)
NEXT i

Julia (2)

cr=-.1
ci=-1
FOR I=-2 TO 2 STEP 5/600
 col%=0
 FOR R=-2 TO 2 STEP 5/800
  c=0 : b=I : a=R : count%=0
  WHILE ABS(a)<=2 AND ABS(b)<=2 AND count%<20
   c=a*a-b*b+cr
   b=2*a*b  +ci
   a=c
   INCR count%,1
  WEND
  if count%<16 then pset (col%,row%),count%
  INCR col%
 NEXT R
 INCR row%
NEXT I

plain IFS

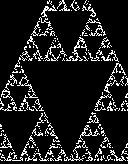
dim a(3,6)
a(1,1)=.5 : a(1,4)=.5 :
a(2,1)=.5 : a(2,4)=.5 : a(2,5)=.5
a(3,1)=.5 : a(3,4)=.5 : a(3,5)=.25 : a(3,6)=.43
for i=0 to 10000
 n=int(rnd*3)+1
 t=a(n,1)*x + a(n,3)*y + a(n,5)
 y=a(n,2)*x + a(n,4)*y + a(n,6)
 x=t
 pset (x*400,y*400),8
next i

Barnsley

x=200
y=0
FOR i=1 TO 10000
 z=RND
 IF z<.02 THEN
  xn=200
  yn=.27*y
 ELSE
  IF z<.17 THEN
   xn=-.139*x+.263*y+228
   yn=.246*x+.224*y+14.4
  ELSE
   IF z<.3 THEN
    xn=.17*x-.215*y+163.2
    yn=.222*x+.176*y+35.72
   ELSE
    xn=.781*x+.034*y+43
    yn=-.032*x+.739*y+108
   END IF
  END IF
 END IF
 PSET(xn-100,400-yn)
 x=xn
 y=yn
NEXT i

IFS

code not available

Dieses Programm ist eine Implementation eines baumähnlichen Fraktals mittels eines iterierten Funktionensystems. Das Programm erzeugt eine s/w Abbildung, die dem nebenstehendenden Bild nur in etwa entspricht.

s = 6
w = 480
xr(s) = w
xo(s) = 0.5 * w
yo(s) = w
a(1) =  0.195 : a(2) =  0.462 : a(3) = -0.058 : a(4) = -0.035 : a(5) = -0.637
b(1) = -0.488 : b(2) =  0.414 : b(3) = -0.07  : b(4) =  0.07  : b(5) =  0
c(1) =  0.344 : c(2) = -0.252 : c(3) =  0.453 : c(4) = -0.469 : c(5) =  0
d(1) =  0.443 : d(2) =  0.361 : d(3) = -0.111 : d(4) = -0.022 : d(5) =  0.501
e(1) =  0.4431: e(2) =  0.2511: e(3) =  0.5976: e(4) =  0.4884: e(5) =  0.8562
f(1) =  0.2452: f(2) =  0.5692: f(3) =  0.0969: f(4) =  0.5069: f(5) =  0.2513
For x = 1 To 5 : e(x) = e(x) * w : f(x) = f(x) * w : Next x
GoSub 2
End
1:
  xl(s) = a(i) * xl(s + 1) + b(i) * yl(s + 1) + e(i)
  yl(s) = c(i) * xl(s + 1) + d(i) * yl(s + 1) + f(i)
  xr(s) = a(i) * xr(s + 1) + b(i) * yr(s + 1) + e(i)
  yr(s) = c(i) * xr(s + 1) + d(i) * yr(s + 1) + f(i)
  xo(s) = a(i) * xo(s + 1) + b(i) * yo(s + 1) + e(i)
  yo(s) = c(i) * xo(s + 1) + d(i) * yo(s + 1) + f(i)
2:
  If s > 1 Then GoTo 3
  Line (xl(1), w - yl(1) + 1)-(xr(1), w - yr(1) + 1)
  Line (xr(1), w - yr(1) + 1)-(xo(1), w - yo(1) + 1)
  Line (xo(1), w - yo(1) + 1)-(xl(1), w - yl(1) + 1)
  Return
3:
  decr s
  i = 1 : GoSub 1
  i = 2 : GoSub 1
  i = 3 : GoSub 1
  i = 4 : GoSub 1
  i = 5 : GoSub 1
  incr s
  Return

Furthermore, in investigating: Is "IFS₁=IFS₂" decidable?, we were able to obtain the following result.

Die Natur will, daß die Kinder Kinder seien,
ehe sie Erwachsene werden.
Jean-Jacques Rousseau