Smooth Subdivision for Mixed Volumetric Meshes

four basic shapes

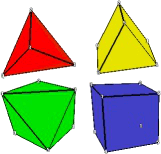
From September 2003 to August 2004, I was involved in research on subdivision algorithms at the computer science department of Rice University in Houston/USA. My thesis is on how to combine uniform volumetric subdivision schemes of cubes, triangular prisms, tetrahedra, and octahedra into a single volumetric scheme.

I derive an algorithm for mixed, unstructured volume meshes consisting of these four types of shapes. In the limit, the scheme yields a parametrization of space that is

• C² smooth everywhere,
• except around extraordinary vertices, and edges, and
• except where a triangle of a prism meets a quad of a prism.

During the two semesters, Scott Schaefer helped me on issues of programming and subdivision. My advisor was Joe Warren.

Smooth Subdivision for Mixed Volumetric Meshes (Thesis)	smooth_subdivis...	3 MB
Subdivision and deformation tool (including C++ source) *	volutil.zip	200 kB

* compiled for Windows. Documentation and examples are included.

Für das Können gibt es nur einen Beweis: das Tun.
Marie von Ebner-Eschenbach

Subdivision of a volume mesh is very similar to subdivision for surfaces. Iteratively, shapes are split into smaller shapes and vertices are positioned according to certain mathematical formulas to make the outcome appear as smooth as possible. Volumetric subdivision induces a C² parametrization of space almost everywhere.

Subdivision for surface meshes inspires volumetric subdivision

Publications related to my thesis are

• Levin, Levin 2003: Analysis of Quasi-Uniform Subdivision
• Warren, Schaefer, Hirani, Desbrun 2003: Barycentric coordinates for convex sets
• Schaefer, Warren 2004: Smooth Subdivision of Tetrahedral Meshes
• Schaefer, Warren 2005: On C^2 Triangle/Quad Subdivision

The thesis is referenced in

• Adi Levin, 2005: The importance of polynomial reproduction in piecewise-uniform subdivision, in Mathematics of Surfaces XI, 11th IMA international Conference, Loughborough/UK

Spinnweben: das Fliegengitter des kleinen Mannes.
Thomas Tonn

Application: Smooth deformations

Besides contextualized space partitioning, the major motivation for volumetric subdivision is to perform smooth deformations of surface models.

Deformation via volumetric subdivision

The deformation procedure requires the following input:

• a surface model like the spoon, which should undergo deformation
• a volumetric mesh that encloses the surface mesh and that controls the deformation

Let 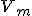be the 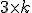matrix consisting of the 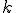vertices of the surface model mesh, that is

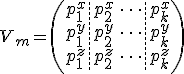
And let 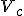be the 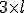matrix consisting of the 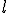vertices of the volumetric control mesh. We are interested in a matrix 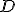that satisfies

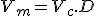
We deform the surface model by changing the vertices of the control mesh to 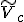. Then, the vertices of the deformed surface model compute as

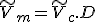
My thesis describes how to obtain 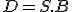as a matrix product, where

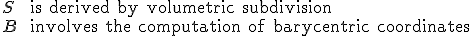
Given the initial meshes, the software that we provide outputs the matrix .

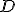To demonstrate the quality of this approach, we deform the model Noma into several poses by designing and altering a volumetric control mesh:

Character animation

please click on the image for more examples

Credits:

• The female model Noma is by courtesy of Mike Beals.
• The 3D-input and haptic device PHANToM was provided to the computer graphics research group by SensAble technologies.

The subdivision algorithm and the deformation results were presented within the scope of the mathematical "Studentische Vortragsreihe 2005" as well as on the 2005 "Workshop" of the geometric modeling research group of the Technische Universität Darmstadt/Germany.

Per aspera ad astra
[translation]