Smoothing using Geodesic Averages

Figure: A sequence of noisy localization estimates of a fast driving go-kart in red, and the result of smoothing in black.

Abstract: Geodesic averages have been used to generalize curve subdivision and Bézier curves to Riemannian manifolds and Lie groups. We show that geodesic averages are suitable to perform smoothing of sequences of data in nonlinear spaces. In applications that produce temporal uniformly sampled manifold data, the smoothing removes high-frequency components from the signal. As a consequence, discrete differences computed from the smoothed sequence are more regular. Our method is therefore a simpler alternative to the extended Kalman filter. We apply the smoothing technique to noisy localization estimates of mobile robots.

Smoothing using Geodesic Averages	smoothing_...pdf	420 kB
Smoothing using Geodesic Averages (on viXra.org)	viXra:1810.0283	link
Smoothing using Geodesic Averages	youtube	link

If you try and take a cat apart to see how it works,
the first thing you have on your hands is a non-working cat.
Douglas Adams

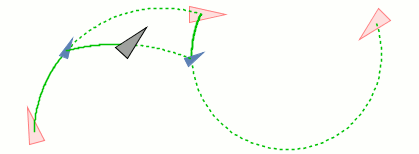
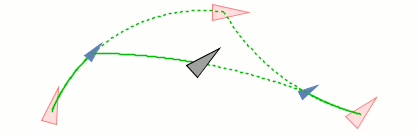
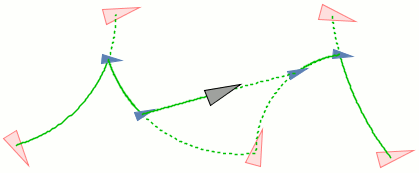
Figure: Geodesic averages in the Lie group SE(2) used in applications: Left, quartic B-spline refinement used in curve subdivision. Center, mean of a 3-point sequence based on Dirichlet weights. Right, mean of a 5-point sequence based on Gaussian weights used for smoothing. The input points are indicated as red arrowheads. The geodesic average is indicated in gray.

The video gives a brief introduction to the topic. For details please refer to the article.

Reality is frequently inaccurate.
Douglas Adams