Curve Subdivision in SE(2)

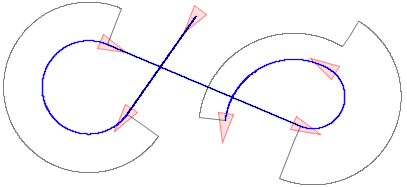
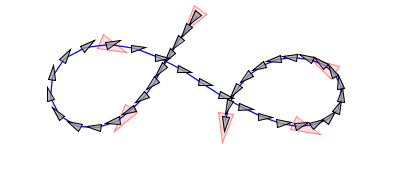
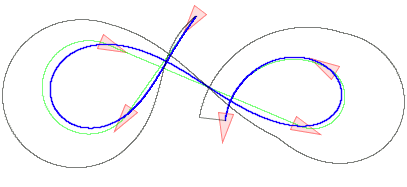
Figure: Dubins path defined by six control points in SE(2). A control point consists of position and heading. The center image shows the result of three rounds of subdivision. Right, the limit curve with continuous curvature. The underlying scheme is cubic B-spline subdivision.

Abstract: We demonstrate that curve subdivision in the special Euclidean group SE(2) allows the design of planar curves with favorable curvature. We state the non-linear formula to position a point along a geodesic in SE(2). Curve subdivision in the Lie group consists of trigonometric functions. When projected to the plane, the refinement method reproduces circles and straight lines. The limit curves are designed by intuitive placement of control points in SE(2).

Curve Subdivision in SE(2)	curve_subdivis...pdf	420 kB
Curve Subdivision in SE(2) (on viXra.org)	viXra:1807.0463	link
Curve Subdivision in SE(2)	youtube	link

Solutions nearly always come from the direction you least expect,
which means there's no point trying to look in that direction
because it won't be coming from there.
The Salmon of Doubt

Für jede Führungskraft wirkt eine gleiche und entgegengesetzte Arbeitskraft.
Third law

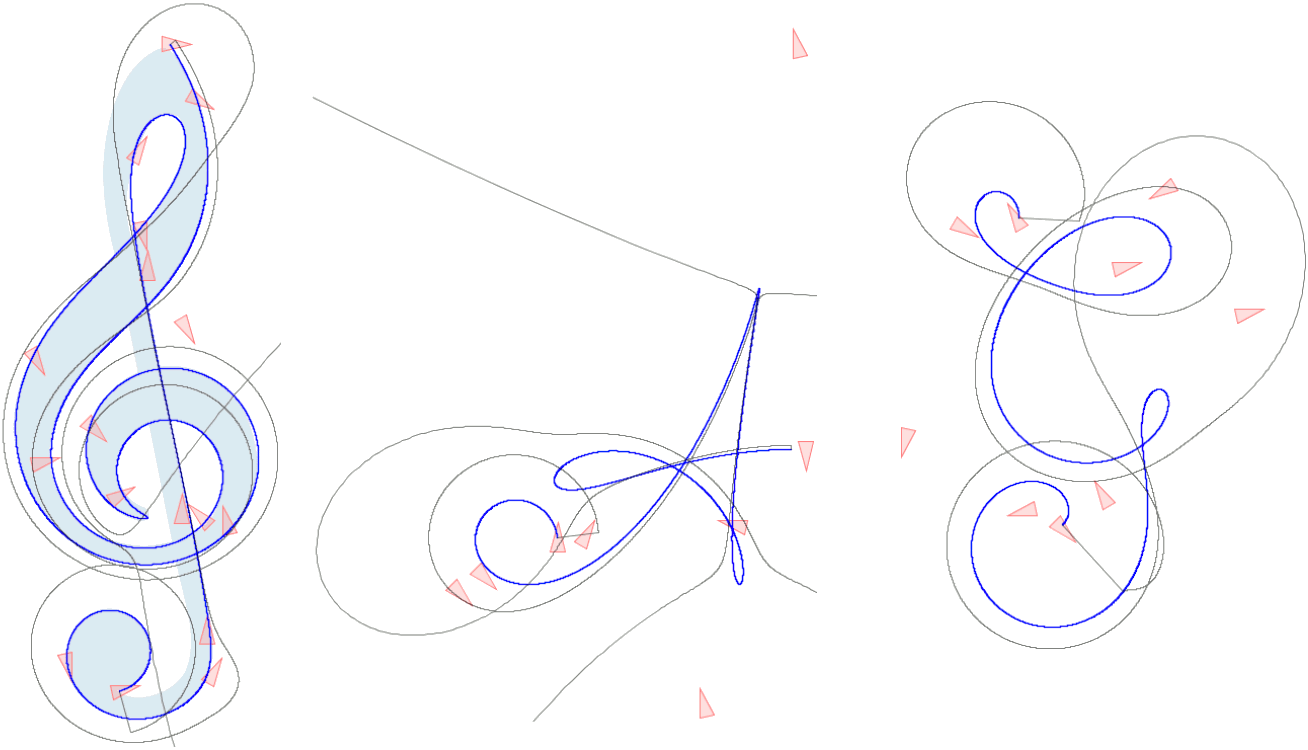
The curves generated by subdivision in SE(2) have applications in robotics as well as glyph design. For details please refer to the article.

Unless you are foolish enough to be continually exited,
you won't have the motivation,
you won't have the energy to carry it through.
God rewards fools.
Martin Hellmann