Gravitational Potential and Spacecraft Orbits

gravitational potential variations on the surface of Earth

Accurate tracking of satellites that have been and are currently orbitting Earth, has lead to a refined approximation of our planets gravitational potential. Conversely, the refined planets gravitational potential yield accurate predictions of satellite orbits.

Because of the radial symmetry, the potential function of the gravitational field is formulated as a spherical harmonic expansion with coefficients j, c, and s (see the details below). The plot aside coutours the potential function at Earths surface level, where rho=r_E, and j(2) is set to zero, to enhance details.

We develop a Mathematica notebook, in order to yield the gradient of the potential function algebraically in Euclidean coordinates. Using the gradient matrix, we employ Runge-Kutta 4-th order integration to compute any satellite orbit in the proximity of Earth.

Remark: MATLAB 7 also supplies a celestial data base - look for "geoid" in the demos.

The gravitational force acting on an object close to Earth, is the negative gradient of the following potential function

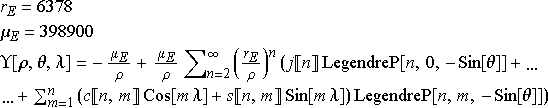
evaluated at

The coefficients j, s, c are distilled from long term observations of trajectories of passive satellites that orbit the Earth. The book Spacecraft System Engineering by Fortescue et al. states the coefficients as

j={0,1082.6*^-6,-2.53*^-6,-1.62*^-6,-0.23*^-6,0.54*^-6}
c={{},{0,1.57*^-6},{-2.19*^-6, 0.31*^-6,-0.1*^-6},{0,0,0,0},{0,0,0,0,0},{0,0,0,0,0,0}};
s={{},{0,-0.9*^-6},{-0.27*^-6,-0.21*^-6,-0.2*^-6},{0,0,0,0},{0,0,0,0,0},{0,0,0,0,0,0}};

Spacecraft orbits (in Mathematica 8) *	satellite_orbits8.nb	40 kB
Spacecraft orbits (in Mathematica 5.2)	satellite_orbits.zip	90 kB

* uses Mathematica's WorldData to plot the countries (instead of a background image), and has fewer example orbits. Successfully tested with Mathematica 10.3.

Hier stehe ich und kann nicht anders.
Martin Luther

Ground tracks and 3D plots of orbits

We plot several instances of satellite ground tracks. The points are spaced equidistantly in time and evolve from yellow to red. Click on the images, for a 3d view of the orbits.

Geostationary Orbit (1964)

• The semi-major axis is 42174.737 km.
• The orbit is circular.
• For the plot below, we choose an inclination of 40 deg, and an westwards offset of 23 deg. Typically the inclination of a geostationary satellite is 0 deg. The orbital period is 1 siderial day, equivalently 86164.1 sec.

Molniya Orbit (1965)

• The semi-major axis is 26450 km.
• The orbit has an eccentricity of 0.722.
• The inclination is 63.4 deg.
• In the plot, the points mark a time elaps of 10 minutes. We track 2 orbits.

Global Positioning System (1985)

• The altidude of each of the 24 space vehicles providing the GPS signal is 20200 km.
• The satellites are distributed equally among six circular orbital planes, which have an inclination of approximately 55° and are separated by 60°.
• In the plot, the points are 1 hour appart. We show 2 orbits.

International Space Station (1998)

• The altitude of the orbit of the ISS is 370 km, resulting in a semi-major axis of r_E + 370 km = 6748.14 km.
• The orbit has an eccentricity of 0, that is, the orbit is circular.
• The inclination is about 51 deg.
• In the plot, the points mark a time elaps of 5 minutes. We track 2 orbits.

Galileo Positioning System (2005)

• There are plans to operate 30 spacecrafts at an orbital altitude of 23222 km.
• The satellites are distributed among three circular orbital planes, which have an inclination of 56°. There will be 9 operational satellites and one active spare per orbital plane.
• In the plot, the points are 1 hour appart. We track 3 orbits.

Pichler-Hakenberg orbit (2007)

• The orbit ranges from 307.5 to 15783.3 km in altitude.
• In the plot, the points are 15 minutes appart. We track 2 orbits.
• View the latitude-altitude plot here.
• The following report analyses the encountered space environments, and their effect on a spacecraft on the Pichler-Hakenberg orbit.

There's nothing out there.
That's why it's called space.
Carl Sagan