Numerics

Numerics provides approximate answers to real world problems.

Toolpath Design and Milling Simulation
Visualization of BPSK Demodulation
Tracking on Homogeneous Manifolds
Sphere-fit to a set of points
Triangulations of elemental shapes in Matlab
There never will be any good, general methods for
solving systems of more than one nonlinear equation.
Press, Teukolsky, Vetterling, Flannery

Tracking on Homogeneous Manifolds

We present a computation to yield the transformation that matches best two given sets of landmarks on a linearized homogeneous manifold. The method allows to restrict the set of feasible transformations in a way that is most relevant in practical applications. If the homogeneous manifold is a vector space, the transformation is optimal in the limit.

Tracking of a differential-drive robot

Input: transitions of correlated landmarks perceived by a differential-drive robot after a short lapse of time (with noise in the measurements)

Output: linear transformation that is consistent with the transitions and the mobility of the robot: driving forward and turning, but no slipping to the side

Time is nature's way of keeping
everything from happening at once.
Allen Stewart Königsberg
Tracking on Homogeneous Manifolds tracking_on_hom... 180 kB
Examples and illustrations (Mathematica 5.2) * tracking.nb 35 kB
* includes an implementation of the Campbell-Baker-Hausdorff formula

Our computation is an alternative to the conventional algorithms in tracking (that might utilize quaternions, or Euler-angles). Our method minimizes the sum of squared errors between the pairs of landmarks in the match. The number of variables is precisely the dimensions of the mobility of the robot. To solve the non-linear equations, Newtons iteration works well.

Tracking of a robot in 3d

Input: correlated landmarks in 3d (with noise in the measurements)

Output: in this example, the robot is free to rotate, but can translate only along the first axis

In the paper, Meshless Deformations Based on Shape Matching by M. Mueller, B. Heidelberger, M. Teschner, M. Gross an optimal rotation is found via the polar decomposition of a matrix. This motivated me to make a tracking algorithm using the Campbell-Baker-Hausdorff series in the more general context of homogeneous manifolds.

If everything seems under control,
you're just not going fast enough.
Mario Andretti

Sphere-fit to a set of points


Example for n=2 and m=5

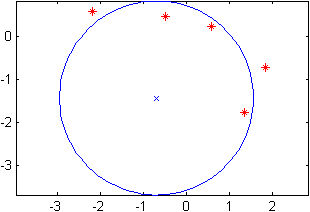
Given a set of points, we find the center and radius of a sphere that fits the points well. The method is extracted from code of Izhak Bucher.

In 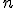dimensional Euclidean space, points on a sphere with center 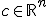and radius 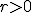are characterized by

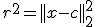
Equivalently,

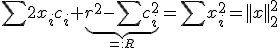
where the summations are over the coordinates 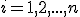. Now, we are given a set of 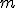points

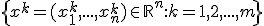
To obtain the center of the fitting sphere 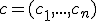, we solve the following system of linear equations in the least square sense

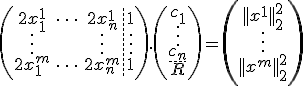
Then, the radius of the sphere is

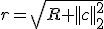
If the matrix above does not have maximum rank, we define .


Example for n=2 and m=3

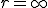As desired, the radius of the sphere is invariant under affine transformation of the points, while the center of the sphere undergoes the same affine transformation. The method is implemented by the following function in Matlab, download. 

function [c,r]=spherefit(X,draw)                % code by jph
%syntax:   [C,R]=SPHEREFIT(X,DRAW)
% X is of size [m n] and contains m points of dimension n.
% C is the center, and R is the radius of the fitting sphere.
% If DRAW is specified and n==2, the result is plotted.
%example:  [c,r]=spherefit(randn(7,2),1)

n=size(X,2);
A=[2*X ones(size(X,1),1)];

if rank(A)<n+1
  c=[];
  r=Inf;
  return;
end

a=A\sum(X.*X,2);
c=a(1:end-1);
r=sqrt(a(end)+c'*c);

if nargin>1&&n==2
  plot(X(:,1),X(:,2),'r*'); 
  hold on; axis equal;
  plot(c(1),c(2),'bx');
  t=linspace(0,2*pi);
  plot(r*cos(t)+c(1),r*sin(t)+c(2),'b');  
  hold off;
end

The following example corresponds to the two dimensional scenario.

To infinity and beyond.
Buzz Lightyear

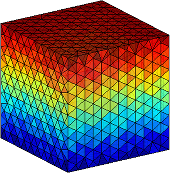
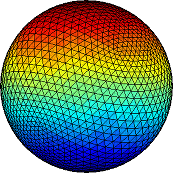
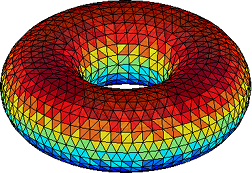
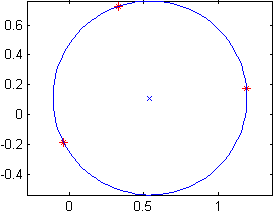
Triangulations of elemental shapes in Matlab

We release Matlab code to create triangulations of four basic shapes in three dimensions: cube, cylinder, sphere, torus. The functions are 

[T,X,Y,Z]=tricube(n);
[T,X,Y,Z]=tricylinder(n);
[T,X,Y,Z]=trisphere(n);
[T,X,Y,Z]=tritorus(R/r,n);

The parameter n controls the granularity. The generation of the torus requires an additional parameter: the ratio of the big and small radius R/r. To visualize the outputs simply use the Matlab command 

trimesh(T,X,Y,Z);
Triangulations of elemental shapes in Matlab * trishapes.zip 50 kB
* for a demo run tridemo.m in Matlab. The triangulation of a sphere only works on Windows.
Nullius in verba