1.4(1).2

In [Ko01] p.65, the homogeneous pair (g,h) with index 1.4(1).2 is defined as

e_1 u_1 u_2 u_3 u_4
e_1 0 0 u_1 u_2 e_1
u_1 0 0 0 0 p u_1
u_2 -u_1 0 0 0 (-1 + p) u_2
u_3 -u_2 0 0 0 (-2 + p) u_3
u_4 -e_1 -p u_1 (1 - p) u_2 (2 - p) u_3 0

for p∈R. Any ρ-invariant scalarproduct B is of the form

Clear[B] ;

B = LSolve[ΗadInv[ad, B = Τℊ★[g, 4], 0], B] ;

MF[B = B/.Vars[B] → {a, b, c, d, e, f}]

( {{0, 0, -a, 0}, {0, a, 0, 0}, {-a, 0, b, c}, {0, 0, c, d}} )

The tensor ν:g×g→m is determined by

Showν[ΗΡν[ad, B], bas]

e_1 u_1 u_2 u_3 u_4
e_1 0 0 u_1/2 u_2/2 0
u_1 0 0 0 (c (-1 + p) u_1)/d + (a (-1 + p) u_4)/d 1/2 (-2 + p) u_1
u_2 u_1/2 0 ((c - c p) u_1)/d + ((a - a p) u_4)/d 0 1/2 (-1 + p) u_2
u_3 u_2/2 (c (-1 + p) u_1)/d + (a (-1 + p) u_4)/d 0 -(b c (-2 + p) u_1)/(a d) - (b (-2 + p) u_4)/d ((c^2 + b d - c^2 p) u_1)/(a d) + (p u_3)/2 + ((c - c p) u_4)/d
u_4 0 1/2 (-2 + p) u_1 1/2 (-1 + p) u_2 ((c^2 + b d - c^2 p) u_1)/(a d) + (p u_3)/2 + ((c - c p) u_4)/d -(c (-2 + p) u_1)/a

The Levi-Civita connection Λ:g→gl(m) is determined by

ShowΛ[ΗΡΛ[ad, B]]

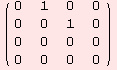Λ_ (j, 1)^i ( {{0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 0}, {0, 0, 0, 0}} )
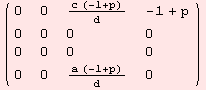Λ_ (j, 2)^i ( {{0, 0, (c (-1 + p))/d, -1 + p}, {0, 0, 0, 0}, {0, 0, 0, 0}, {0, 0, (a (-1 + p))/d, 0}} )
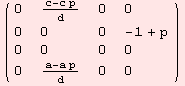Λ_ (j, 3)^i ( {{0, (c - c p)/d, 0, 0}, {0, 0, 0, -1 + p}, {0, 0, 0, 0}, {0, (a - a p)/d, 0, 0}} )
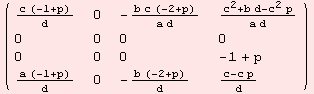Λ_ (j, 4)^i ( {{(c (-1 + p))/d, 0, -(b c (-2 + p))/(a d), (c^2 + b d - c^2 p)/(a d)}, {0, 0, 0, 0}, {0, 0, 0, -1 + p}, {(a (-1 + p))/d, 0, -(b (-2 + p))/d, (c - c p)/d}} )
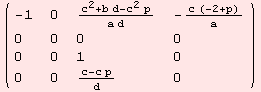Λ_ (j, 5)^i ( {{-1, 0, (c^2 + b d - c^2 p)/(a d), -(c (-2 + p))/a}, {0, 0, 0, 0}, {0, 0, 1, 0}, {0, 0, (c - c p)/d, 0}} )

The non-zero evaluations of the Riemannian-curvature tensor R:m×m→gl(m) are determined by

Showℛ[ℛ = ΗΡℛ[ad, B]]

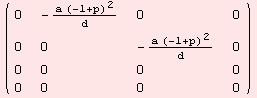ℛ_ (1, 2, j)^i ( {{0, -(a (-1 + p)^2)/d, 0, 0}, {0, 0, -(a (-1 + p)^2)/d, 0}, {0, 0, 0, 0}, {0, 0, 0, 0}} )
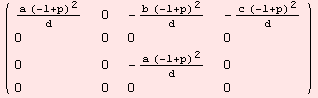ℛ_ (1, 3, j)^i ( {{(a (-1 + p)^2)/d, 0, -(b (-1 + p)^2)/d, -(c (-1 + p)^2)/d}, {0, 0, 0, 0}, {0, 0, -(a (-1 + p)^2)/d, 0}, {0, 0, 0, 0}} )
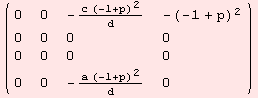ℛ_ (1, 4, j)^i ( {{0, 0, -(c (-1 + p)^2)/d, -(-1 + p)^2}, {0, 0, 0, 0}, {0, 0, 0, 0}, {0, 0, -(a (-1 + p)^2)/d, 0}} )
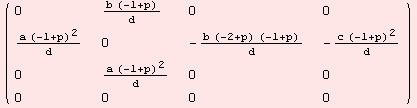ℛ_ (2, 3, j)^i ( {{0, (b (-1 + p))/d, 0, 0}, {(a (-1 + p)^2)/d, 0, -(b (-2 + p) (-1 + p))/d, -(c (-1 + p)^2)/d}, {0, (a (-1 + p)^2)/d, 0, 0}, {0, 0, 0, 0}} )
ℛ_ (2, 4, j)^i ( {{0, 0, 0, 0}, {0, 0, -(c (-1 + p)^2)/d, -(-1 + p)^2}, {0, 0, 0, 0}, {0, (a (-1 + p)^2)/d, 0, 0}} )
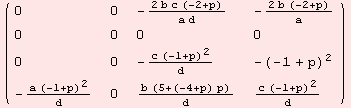ℛ_ (3, 4, j)^i ( {{0, 0, -(2 b c (-2 + p))/(a d), -(2 b (-2 + p))/a}, {0, 0, 0, 0}, {0, 0, -(c (-1 + p)^2)/d, -(-1 + p)^2}, {-(a (-1 + p)^2)/d, 0, (b (5 + (-4 + p) p))/d, (c (-1 + p)^2)/d}} )

The Ricci-curvature Ric:m×m→R is determined by

MF[Ric = ΜRic[ℛ]]

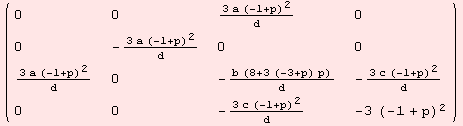
( {{0, 0, (3 a (-1 + p)^2)/d, 0}, {0, -(3 a (-1 + p)^2)/d, 0, 0}, {(3 a (-1 + p)^2)/d, 0, -(b (8 + 3 (-3 + p) p))/d, -(3 c (-1 + p)^2)/d}, {0, 0, -(3 c (-1 + p)^2)/d, -3 (-1 + p)^2}} )

We demand Ric=0. Thus, b=0 and p=1.

sol = Union[Solve[Ric≡0]]

Solve :: svars : Equations may not give solutions for all \"solve\" variables. Mehr…

{{b→0, p→1}}

But then, the Riemannian curvature tensor vanishes also.

Showℛ[ℛ/.sol[[1]]]

ℛ-Flat

Note, this result is independent of the signature of B.

Created by Mathematica  (August 15, 2006) Valid XHTML 1.1!