1.1(2).8

In [Ko01] p.48, the homogeneous pair (g,h) with index 1.1(2).8 is defined as

ShowAd[ad = Table2ad[bas = {e_1, u_1, u_2, u_3, u_4}, ( {{0, u_3, 0, -u_1, 0}, {-u_3, 0, 0, 0, 0}, {0, 0, 0, 0, u_2}, {u_1, 0, 0, 0, 0}, {0, 0, -u_2, 0, 0}} )], 4]

e_1 u_1 u_2 u_3 u_4
e_1 0 u_3 0 -u_1 0
u_1 -u_3 0 0 0 0
u_2 0 0 0 0 u_2
u_3 u_1 0 0 0 0
u_4 0 0 -u_2 0 0

Any ρ-invariant scalarproduct B is of the form

Clear[B] ;

B = LSolve[ΗadInv[ad, B = Τℊ★[g, 4], 0], B] ;

MF[B = B/.Vars[B] → {b, c, a, d, e, f}]

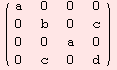
( {{a, 0, 0, 0}, {0, b, 0, c}, {0, 0, a, 0}, {0, c, 0, d}} )

The tensor ν:g×g→m is determined by

Showν[ΗΡν[ad, B], bas]

e_1 u_1 u_2 u_3 u_4
e_1 0 u_3/2 0 -u_1/2 0
u_1 u_3/2 0 0 0 0
u_2 0 0 (b c u_2)/(-c^2 + b d) + (b^2 u_4)/(c^2 - b d) 0 (1/2 + c^2/(-c^2 + b d)) u_2 + (b c u_4)/(c^2 - b d)
u_3 -u_1/2 0 0 0 0
u_4 0 0 (1/2 + c^2/(-c^2 + b d)) u_2 + (b c u_4)/(c^2 - b d) 0 (c d u_2)/(-c^2 + b d) + (c^2 u_4)/(c^2 - b d)

The Levi-Civita connection Λ:g→gl(m) is determined by

ShowΛ[ΗΡΛ[ad, B]]

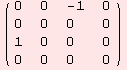Λ_ (j, 1)^i ( {{0, 0, -1, 0}, {0, 0, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 0}} )
Λ_ (j, 2)^i zero…4×4
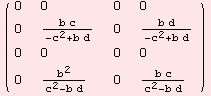Λ_ (j, 3)^i ( {{0, 0, 0, 0}, {0, (b c)/(-c^2 + b d), 0, (b d)/(-c^2 + b d)}, {0, 0, 0, 0}, {0, b^2/(c^2 - b d), 0, (b c)/(c^2 - b d)}} )
Λ_ (j, 4)^i zero…4×4
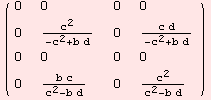Λ_ (j, 5)^i ( {{0, 0, 0, 0}, {0, c^2/(-c^2 + b d), 0, (c d)/(-c^2 + b d)}, {0, 0, 0, 0}, {0, (b c)/(c^2 - b d), 0, c^2/(c^2 - b d)}} )

The non-zero evaluations of the Riemannian-curvature tensor R:m×m→gl(m) are determined by

Showℛ[ℛ = ΗΡℛ[ad, B]]

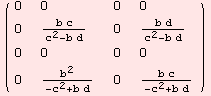ℛ_ (2, 4, j)^i ( {{0, 0, 0, 0}, {0, (b c)/(c^2 - b d), 0, (b d)/(c^2 - b d)}, {0, 0, 0, 0}, {0, b^2/(-c^2 + b d), 0, (b c)/(-c^2 + b d)}} )

The Ricci-curvature Ric:m×m→R is determined by

MF[Ric = ΜRic[ℛ]]

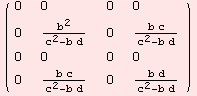
( {{0, 0, 0, 0}, {0, b^2/(c^2 - b d), 0, (b c)/(c^2 - b d)}, {0, 0, 0, 0}, {0, (b c)/(c^2 - b d), 0, (b d)/(c^2 - b d)}} )

We demand Ric=0. Thus, b=0.

sol = Union[Solve[Ric≡0]]

Solve :: svars : Equations may not give solutions for all \"solve\" variables. Mehr…

{{b→0}}

But then, the Riemannian curvature tensor vanishes also.

Showℛ[ℛ/.sol[[1]]]

ℛ-Flat

Note, this result is independent of the signature of B.

Created by Mathematica  (August 15, 2006) Valid XHTML 1.1!