index_42.html

Classification 1 of 1

In the previous section, we have derived the geometric tensors, in particular Ric=0, for the following scalar-product, to which we now apply the Lie-Algebra automorphisms:

$Τα[( {{0, 0, b_7, -b_6}, {0, 0, b_6, b_7}, {b_7, b_6, b_8, b_9}, {-b_6, b_7, b_9, b_10}} ), 0, EXP[λ M[[1]]]]//MF$

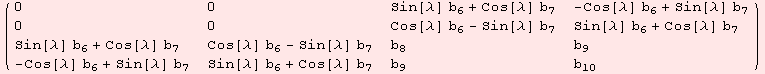
$Τα[( {{0, 0, b_7, -b_6}, {0, 0, b_6, b_7}, {b_7, b_6, b_8, b_9}, {-b_6, b_7, b_9, b_10}} )/.{b_6→0}, 0, EXP[λ M[[3]]]]//MF$

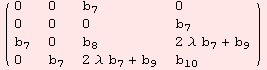
$( {{0, 0, b_7, 0}, {0, 0, 0, b_7}, {b_7, 0, b_8, 2 λ b_7 + b_9}, {0, b_7, 2 λ b_7 + b_9, b_10}} )$

$Τα[( {{0, 0, b_7, -b_6}, {0, 0, b_6, b_7}, {b_7, b_6, b_8, b_9}, {-b_6, b_7, b_9, b_10}} )/.{b_6→0, b_9→0}, 0, EXP[λ M[[4]]]]//MF$

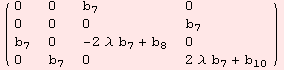
$( {{0, 0, b_7, 0}, {0, 0, 0, b_7}, {b_7, 0, -2 λ b_7 + b_8, 0}, {0, b_7, 0, 2 λ b_7 + b_10}} )$

$Τα[( {{0, 0, b_7, -b_6}, {0, 0, b_6, b_7}, {b_7, b_6, b_8, b_9}, {-b_6, b_7, b_9, b_10}} )/.{b_6→0, b_9→0, b_8→0}, 0, EXP[λ M[[2]]]]//MF$

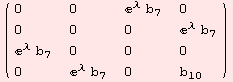
$( {{0, 0, ^λ b_7, 0}, {0, 0, 0, ^λ b_7}, {^λ b_7, 0, 0, 0}, {0, ^λ b_7, 0, b_10}} )$

We state the non-isomorphic pairs:

$ShowSol[A12, ( {{0, 0, b_7, -b_6}, {0, 0, b_6, b_7}, {b_7, b_6, b_8, b_9}, {-b_6, b_7, b_9, b_10}} ), {b_6→0, b_9→0, b_8→0, b_7→1}]$

$We consider the Lie-algebra with commutator<br /> ad = ( {{0, 0, e_1, -e_2}, {0, 0, e_2, e_1}, {-e_1, -e_2, 0, 0}, {e_2, -e_1, 0, 0}} )$

$and the scalar product of the form ℬ = ( {{0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}, {0, 1, 0, b_10}} )$

$Then, the non-zero evaluations of the Riemannian curvature tensor are determined by<br /> {{RIE_ (3, 4, j)^i, ( {{0, 0, 0, -b_10}, {0, 0, b_10, 0}, {0, 0, 0, 0}, {0, 0, 0, 0}} )}}$

$ShowSol[A12, ( {{0, 0, b_7, -b_6}, {0, 0, b_6, b_7}, {b_7, b_6, b_8, b_9}, {-b_6, b_7, b_9, b_10}} ), {b_6→0, b_9→0, b_8→0, b_7→ -1}]$

$We consider the Lie-algebra with commutator<br /> ad = ( {{0, 0, e_1, -e_2}, {0, 0, e_2, e_1}, {-e_1, -e_2, 0, 0}, {e_2, -e_1, 0, 0}} )$

$and the scalar product of the form ℬ = ( {{0, 0, -1, 0}, {0, 0, 0, -1}, {-1, 0, 0, 0}, {0, -1, 0, b_10}} )$

$Then, the non-zero evaluations of the Riemannian curvature tensor are determined by<br /> {{RIE_ (3, 4, j)^i, ( {{0, 0, 0, b_10}, {0, 0, -b_10, 0}, {0, 0, 0, 0}, {0, 0, 0, 0}} )}}$

Created by Mathematica (September 15, 2007)