Investigation: b_1≠0

We reduce the scalar product: By applying a Lie-algebra automorphism, we yield the implication b_1≠0⇒b_3=0.

subst = {b_2→0, b_3→0} ;

Τα[B/.subst, 0, EXP[λ M[[4]]]/.λ→λ]//MF

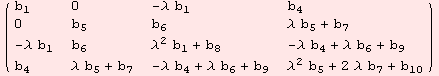
We compute the geometric tensors:

eqs = ShowGeo[{b_2→0, b_3→0}] ;

We consider the scalar product ℬ = ( {{b_1, 0, 0, b_4}, {0, b_5, b_6, b_7}, {0, b_6, b_8, b_9}, {b_4, b_7, b_9, b_10}} )

with determinant<br /> |ℬ| = b_4^2 (b_6^2 - b_5 b_8) - b_1 (b_7^2 b_8 - 2 b_6 b_7 b_9 + b_5 b_9^2 + (b_6^2 - b_5 b_8) b_10)

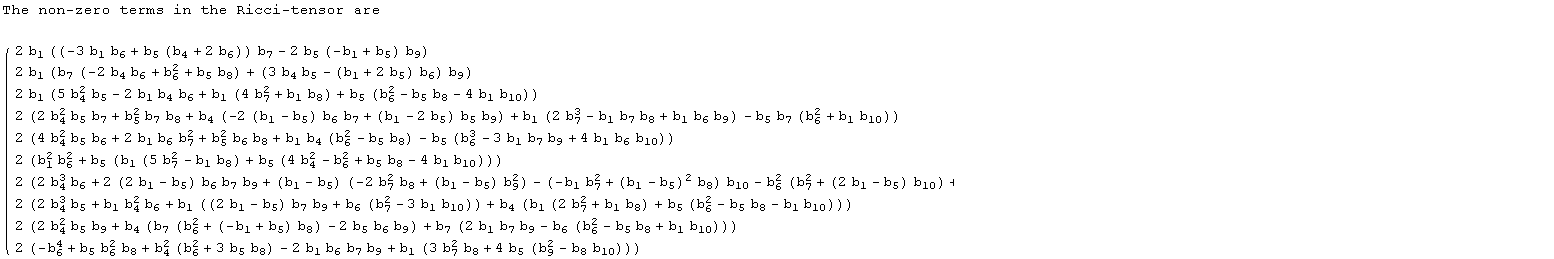
The conditions det[B]≠0, and Ric=0 imply

Reduce[eqs]

But b_1==0 is a contradiction to our assumption b_1≠0.

Created by Mathematica  (September 15, 2007) Valid XHTML 1.1!