is defined via the adjoint map (1,2)-tensor ad.
A4,10
The Lie-algebra is defined via the adjoint map (1,2)-tensor ad.
![A10 = ad = Table2ad[2 Τ[({{0, 0, 0, 0}, {0, 0, e_1, -e_3}, {0, 0, 0, e_2}, {0, 0, 0, 0}})]] ; [adJacobi[ad]] ;](../HTMLFiles/index_276.gif)
The automorphism group of the Lie-algebra is generated by the following matrices:
![M = Algebra[4, Τdα[ad, 1, #1] &, ] ;](../HTMLFiles/index_277.gif){kind=small}
![ShowMat[EXP[λ #1] &/@M]](../HTMLFiles/index_278.gif){kind=small}
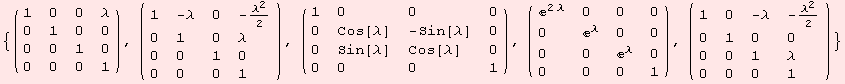
We reduce the scalar product: Due to the Lie-algebra automorphism α, we may assume 
=0.
![α = ( {{1, 0, 0, 0}, {0, Cos[λ], -Sin[λ], 0}, {0, Sin[λ], Cos[λ], 0}, {0, 0, 0, 1}} ) ;](../HTMLFiles/index_281.gif)
![Τα[B, 0, α]//MF](../HTMLFiles/index_282.gif){kind=small}
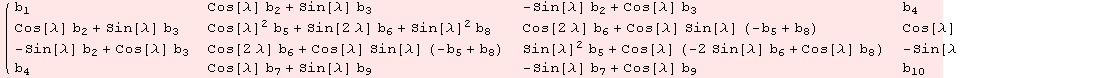
| Created by Mathematica (September 15, 2007) |  |
