Inverse Distance Coordinates for Scattered Sets of Points

Inverse Distance Weighting [1968 Shepard]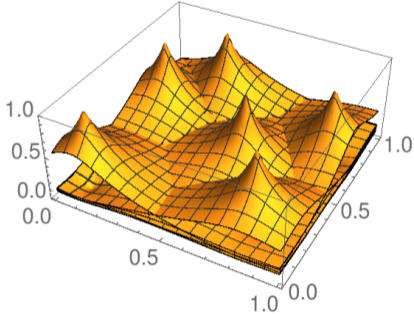

Affine Coordinates [2011 Waldron]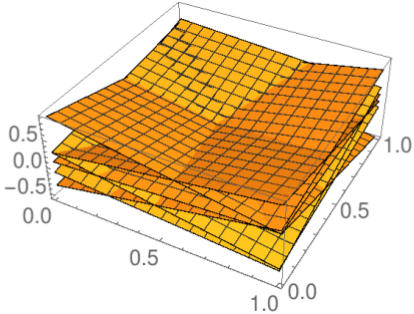

Inverse Distance Coordinates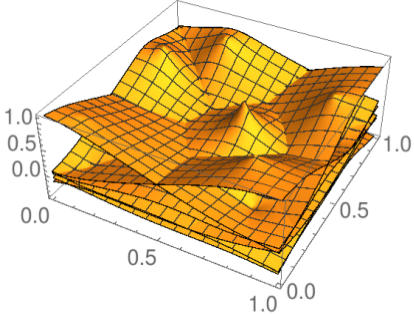

Figure: Basis functions of inverse distance weighting, affine coordinates, and inverse distance coordinates for an example set of six points in the plane.

Abstract: We present meshfree generalized barycentric coordinates for scattered sets of points in d-dimensional vector space. The coordinates satisfy the Lagrange property. Our derivation is based on the projection of Shepard's popular inverse distance weights to their best fit in the subspace of coordinates with linear reproduction. The notion of distance between a pair of points is sufficient for the construction of coordinates.

Inverse Distance Coordinates for Scattered Sets of Points	inverse_distanc...pdf	1.2 MB
	viXra:2002.0129	link

If life is going to exist in a Universe of this size,
then the one thing it cannot afford to have is a sense of proportion.
Douglas Adams

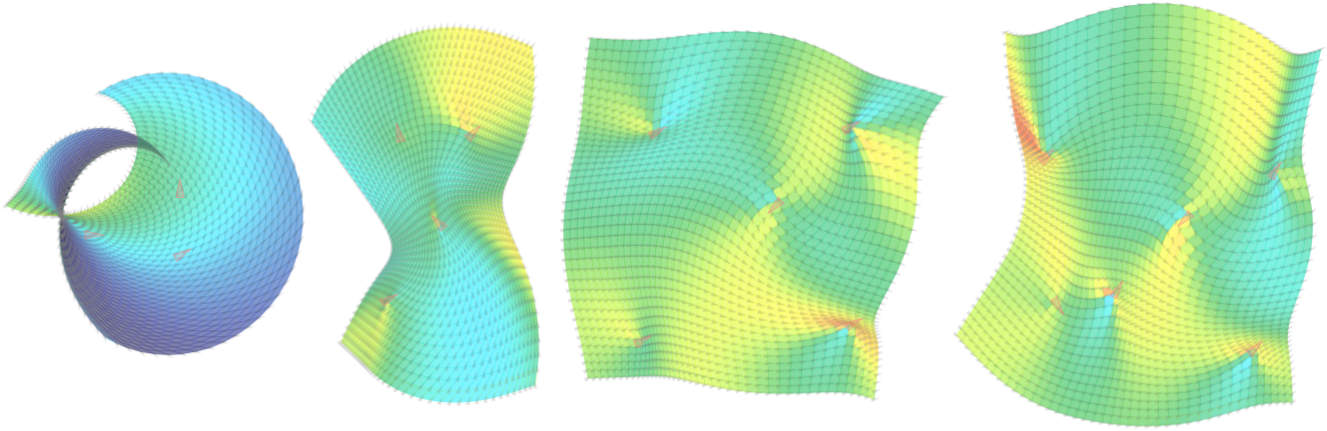
Figure: The graphics show the evaluation of inverse distance coordinates for input sets of points from the plane for n=3,4,5,6, respectively, that have associated values in the 3-dimensional Lie group SE(2) Covering. The coordinates are evaluated over a rectangular domain that covers the point sets and mapped into the Lie group using the formulas derived in [2006 Arsigny, Pennec, Ayache]. Elements from the Lie group are plotted as arrowheads.

All the planning charts and demolition orders have been on display
at your local planning department in Alpha Centauri for 50 of your Earth years,
so you've had plenty of time to lodge any formal complaint
and it's far too late to start making a fuss about it now.
The Hitchhiker's Guide to the Galaxy

The author was partially supported by personal savings accumulated during his employment at ETH Zürich in 2017–2019. He'd like to thank everyone who worked to make this opportunity available to him.