
Wir formulieren das Verhalten zweier starrer Körper bei einem elastischen Stoß mathematisch. Auf die Fragestellung wurde ich bei einer Spielentwicklung aufmerksam. Über drei Jahre lang ließ sich keine zufriedenstellende Lösung weder in Büchern noch im Internet finden. Während eines Semesters in Kiruna hatte ich endlich die Möglichkeit, das Problem selber zu untersuchen.
Die Eingabe zu dem Problem sind:
Ohne Beschränkung der Allgemeinheit nehmen wir an:
Wir möchten
Schritt für Schritt leiten wir eine Lösung des Problems her. Das Computerprogramm, das die Stöße simuliert und darstellt, steht zum Download zur Verfügung. Für die Differentialgleichungen der Rotation genügt einfache Euler-Integration.
| Rigid Body Collision Resolution (C++) * |
|
230 kB |
It might be the warriors who get the glory,
but it's the engineers who build societies.
B'Elanna Torres
Einleitend werden wir in diesem Abschnitt Kraft und Drehmoment vorschlagen, die wärend einer Kollision anliegen sollen. Dabei müssen natürlich der totale lineare Impuls als auch der totale Drehimpuls erhalten bleiben. Innerhalb dieses vorläufigen Modells gestatten wir, daß die Körper sich für eine kurze Zeit überschneiden. Kraft und Drehmoment, die während der Kollision anliegen, sorgen für die Trennung der Körper.
In den Illustrationen stellt ein Ellipsoid den Trägheitsmoment eines Körpers dar. Der Ellipsoid ist nicht identisch mit dem Äußeren des Körpers.

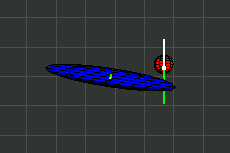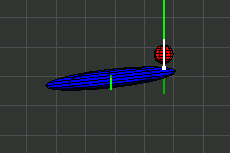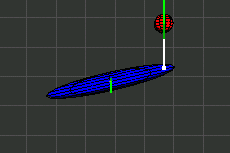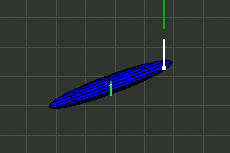
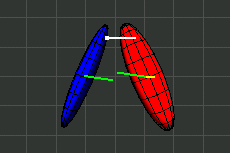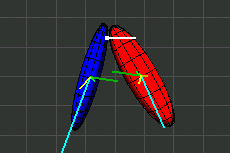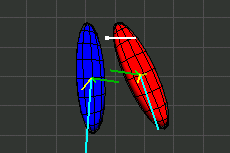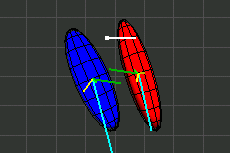
Wahrscheinlich sind dem Leser die folgenden Ausdrücke bekannt.
Wir nummerieren die starren Körper mit
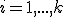 .
Jeder Körper hat
.
Jeder Körper hat

Wir vergegenwärtigen uns noch einmal die Annahmen. Den Masseschwerpunkt haben wir in den Nullpunkt gelegt,
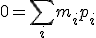
und der total lineare Impuls ist der Nullvektor
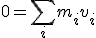
Wir behandeln die Menge der Körper als ein geschlossenes System. Innerhalb dieses Systems bleiben der totale lineare Impuls und der totale Drehimpuls erhalten. Diese Größen sind also zu jeder Zeit konstante Vektoren.
Der totale lineare Impuls ist die Summe der linearen Impulse der einzelnen Körper
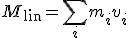
Der totale Drehimpuls ist die Summe der Drehimpulse der einzelnen Körper mit Bezug auf den totalen Masseschwerpunkt
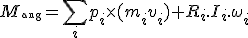
Da in unserer Welt die totalen Impulse konstant sind, ist ihre zeitliche Ableitung der Nullvektor. Die Gleichungen, die das formulieren, sind
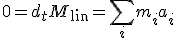
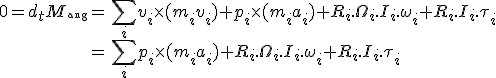
In dieser Herleitung nehmen wir an, daß alle Größen zeitabhängig sind, außer Masse und das Trägheitsmoment. Die eingeführten Variablen bedeuten:
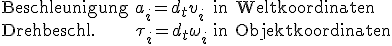
während
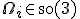 die Drehgeschwindigkeit in Matrixform darstellt.
die Drehgeschwindigkeit in Matrixform darstellt.
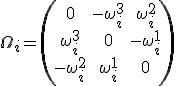
Wir interessieren uns für Kraft und Drehmoment, die während der Überschneidung an den Körpern anliegen. Dafür spezialisieren wir die Formeln auf zwei Körper.
Es gelte 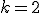 .
Wir führen nun Symbole ein, die den Kontakt zwischen den beiden Körpern charakterisieren:
.
Wir führen nun Symbole ein, die den Kontakt zwischen den beiden Körpern charakterisieren:
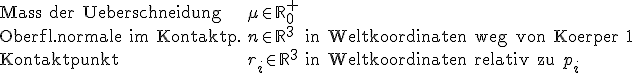
Wenn wir uns vorstellen, daß sich die Körper für eine kurze Zeit überschneiden, dann sei
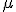 proportional zu der gegenwärtigen Eindringtiefe.
Während die Körper sich nicht berühren, soll
proportional zu der gegenwärtigen Eindringtiefe.
Während die Körper sich nicht berühren, soll
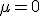 gelten.
Wir schlagen vor, die folgenden Kräfte und Drehmomente anzulegen
gelten.
Wir schlagen vor, die folgenden Kräfte und Drehmomente anzulegen
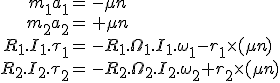
Wir zeigen, daß unter diesen Bedingungen sowohl der totale lineare Impuls als auch der totale Drehimpuls unverändert bleiben. Erhalt des totalen linearen Impulses folgt weil
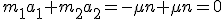
Der totale Drehimpuls ändert sich nicht weil
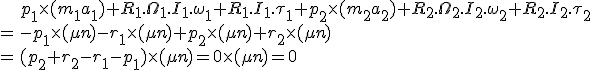
Diese Formeln führen zu den oben gezeigten Animationen.
Man muss wissen, bis wohin man zu weit gehen kann.
Jean Cocteau
Wir erinnern an das in der Einleitung formulierte Ziel: Gegeben seien die Geschwindigkeiten und Drehgeschwindigkeiten kurz vor dem Kontakt. Wir möchten eine Formel, die die Geschwindigkeiten kurz nach dem Kontakt berechnet. In diesem Abschnitt geben wir einen Lösungsvorschlag, der natürlich mit den vorherigen Definitionen und Herleitungen in Einklang ist.
In den Illustrationen stellt ein Ellipsoid den Trägheitsmoment eines Körpers dar. Der Ellipsoid ist nicht identisch mit dem Äußeren des Körpers.

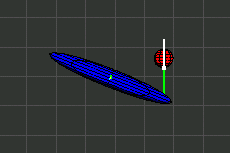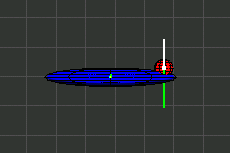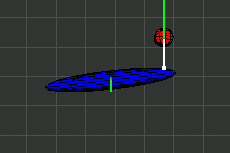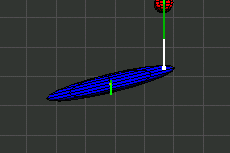

Ich hoffe, daß dem Leser die anstehenden Formeln genauso gefallen wie mir.
Wir führen noch einige Symbole ein
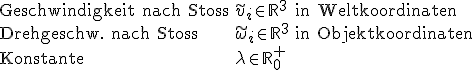
Wir schlagen vor, die Geschwindigkeiten kurz vor dem Kontakt in folgender Weise in die Geschwindigkeiten kurz nach dem Kontakt übergehen zu lassen
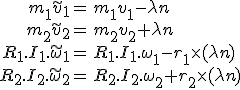
Dabei bleiben der totale lineare Impuls als auch der totale Drehimpuls unverändert: Der Erhalt des gesamt linearen Impulses folgt aus
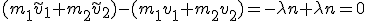
Der totale Drehimpuls nach der Kollision ist
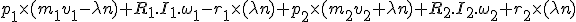
Davon subtrahieren wir den totalen Drehimpuls vor der Kollision
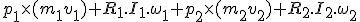
und erhalten eine Differenz von
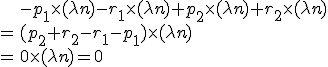
An diesem Punkt verbleibt
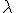 als einzige Unbekannte.
Wir zeigen, daß die Zahl
als einzige Unbekannte.
Wir zeigen, daß die Zahl
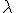 eindeutig festgelegt ist unter der Annahme, daß der Stoß elastisch ist.
eindeutig festgelegt ist unter der Annahme, daß der Stoß elastisch ist.
In einer elastischen Kollision, ist die Bewegungsenergie vor und nach dem Stoß gleich, d.h.
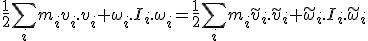
Oben haben wir die folgenden Relationen vorgeschlagen
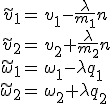
wobei
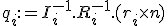
Die Zahl 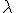 festzulegen, so daß die gesamt Bewegungsenergie erhalten bleibt, bedeutet ein quadratisches Polynom zu lösen. Offensichtlich ist
festzulegen, so daß die gesamt Bewegungsenergie erhalten bleibt, bedeutet ein quadratisches Polynom zu lösen. Offensichtlich ist
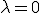 eine Möglichkeit die totale Bewegungsenergie zu erhalten, allerdings bedeutet das, daß gar keine Kollision stattfindet.
Stattdessen interessieren wir uns für
eine Möglichkeit die totale Bewegungsenergie zu erhalten, allerdings bedeutet das, daß gar keine Kollision stattfindet.
Stattdessen interessieren wir uns für
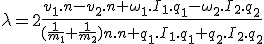
Man beachte, daß der Zähler des Quotienten das Skalarprodukt von der Berührungsgeschwindigkeit im Kontaktpunkt und der Oberflächennormale 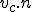 ist, wobei
ist, wobei
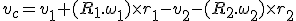
An dieser Stelle sind wir fertig.
Die angegebene Formel für
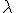 wurde in den Animationen verwendet.
Wir schließen mit einigen Bemerkungen:
wurde in den Animationen verwendet.
Wir schließen mit einigen Bemerkungen:
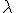 ein wenig zu verkleinern, ist eine komfortable Möglichkeit um den Verlust von Bewegungsenergie zu simulieren.
Der totale lineare Impuls als auch der totale Drehimpuls bleiben trotzdem erhalten.
ein wenig zu verkleinern, ist eine komfortable Möglichkeit um den Verlust von Bewegungsenergie zu simulieren.
Der totale lineare Impuls als auch der totale Drehimpuls bleiben trotzdem erhalten.
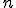 , was eine bequeme Methode ist, inelastische Stöße zu modellieren.
, was eine bequeme Methode ist, inelastische Stöße zu modellieren.
Für eine abschließende Demonstration bedienen wir uns RAPID, einer C-Bibliothek zur Kollisionsdetektion. Die weißen Punkte markieren den letzten Kontaktpunkt.
Wenn du Zeit gewinnen willst,
musst du Zeit verlieren.
Jean-Jacques Rousseau
Eine open-source Physics-Engine, die ich selber ausprobiert habe, ist die Newton Game Dynamics von Julio Jerez und Alain Suero. Die Software stellt eine Demo bereit, die einen das breite Anwendungsspektrum erahnen laesst. Mir erscheinen die Ergebnisse effizient, stabil, and realistisch. Darüberhinaus ist ihr C++ Stil einfach perfekt.
Die Open Dynamics Engine (ODE) initiiert von Russell Smith scheint eine populäre C/C++ library für Spielentwickler zu sein, wird aber auch in der Robotik eingesetzt. Die Bibliothek eigne sich besonders zur Simulation von articulated rigid body structures. Allerdings setzt ODE den Schwerpunkt eher auf Geschwindigkeit als auf physikalische Genauigkeit.
Vor kurzem haben sich Forscher an der Stanford University eine Strategie ausgedacht, um unzählige starre Körper zu animieren und kollidieren zu lassen. Die Veröffentlichung Nonconvex Rigid Bodies with Stacking beschreibt wie sich die atemberaubenden Ergebnisse erzielen lassen. Eine open source Implementation ihrer Methode wurde von Danny Chapman entwickelt und bereitgestellt. Um mehrfach-Montakt und multi-Körper Kollisionen aufzuloesen schlagen die Autoren vor, das Szenario mehrfach zu simulieren: Allerdings jedesmal mit einer veränderten Reihenfolge paarweiser Kollisionen. Danach können die Resultate gemittelt werden.