docu5_lie-groups.nb

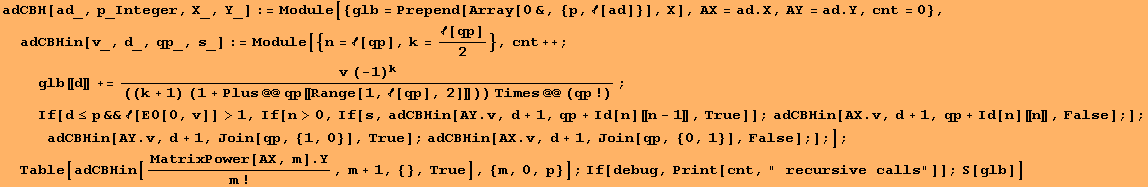
Campbell-Baker-Hausdorff series

First of all, it took hours to get an efficient implementation of the Campbell-Baker-Hausdorff series of a Lie algebra. The result is the function adCBH as you see it below.

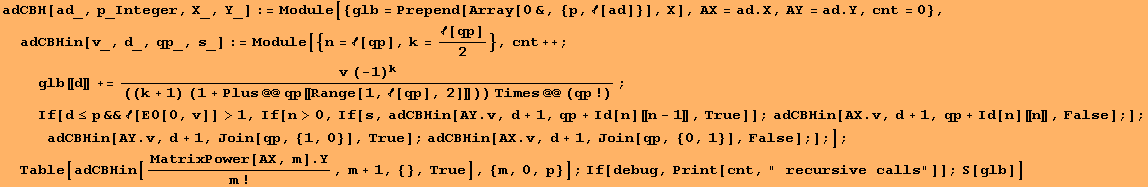
The first terms of the Campbell-Baker-Hausdorff series in math notation are
log(exp(X+Y))=X+Y+ad.X.Y/2-(ad.ad.X.Y.X+ad.ad.Y.X.Y)/12+ad.ad.ad.Y.X.X.Y/24+...
for X,Y∈g. In conventional notation, this translates to
log(exp(X+Y))=X+Y+[X.Y]/2-([[X,Y],X]+[[Y.X],Y])/12+[[[Y,X],X],Y]/24+...

What does it do? It approximates the group action. Example: The n-Heisenberg algebra has dimensions 2n+1 and denote the basis with ,...,,h,,.... Commutator defined by [,]=k.

$ShowAd[ad = adℋℯ[2], {p_1, p_2, h, q_1, q_2}]$

( {{0, 0, 0, h, 0}, {0, 0, 0, 0, h}, {0, 0, 0, 0, 0}, {-h, 0, 0, 0, 0}, {0, -h, 0, 0, 0}} )

n-Heisenberg algebra is nilpotent, so the Campbell-Baker-Hausdorff series converges. In this case, the formula reduces to a finite sum. We identify G=g with action X,Y∈g provided by the Campbell-Baker-Hausdorff series. Below, the group action in coordinates

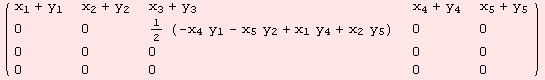
$( {{x_1 + y_1, x_2 + y_2, x_3 + y_3, x_4 + y_4, x_5 + y_5}, {0, 0, 1/2 (-x_4 y_1 - x_5 y_2 + x_1 y_4 + x_2 y_5), 0, 0}, {0, 0, 0, 0, 0}, {0, 0, 0, 0, 0}} )$

${x_1 + y_1, x_2 + y_2, x_3 + y_3 + 1/2 (-x_4 y_1 - x_5 y_2 + x_1 y_4 + x_2 y_5), x_4 + y_4, x_5 + y_5}$

Next example: The ad tensor below, represents the Lie algebra structure of sl(2,R).

$ShowAd[ad = Table2ad[( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} )]]$

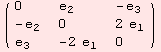
$( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} )$

The algebra is not nilpotent as the descending series does not culminate in {0}.

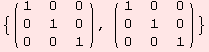
{( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} ), ( {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} )}

The Campbell-Baker-Hausdorff series does not converge:

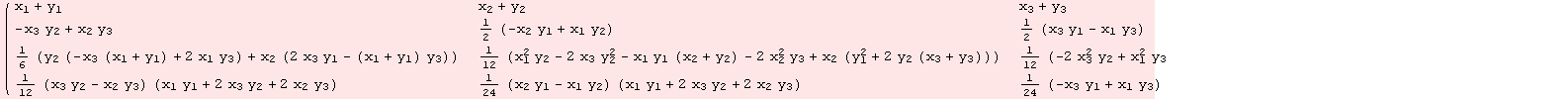
The expansion of the group action in the first coordinate begins with

$1 {x_1 + y_1}$

$2 {-x_3 y_2 + x_2 y_3}$

$3 {1/6 (y_2 (-x_3 (x_1 + y_1) + 2 x_1 y_3) + x_2 (2 x_3 y_1 - (x_1 + y_1) y_3))}$

$4 {1/12 (x_3 y_2 - x_2 y_3) (x_1 y_1 + 2 x_3 y_2 + 2 x_2 y_3)}$

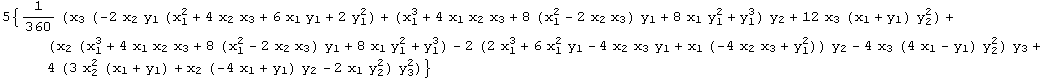
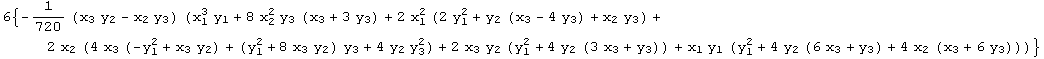
Next example: The commutator table of R is ad below. Up to our knowledge, there does not exist an explicit formula for the group action R in coordinates. To obtain a group action in coordinates would mean to analytically reverse engineer the matrix Z in = depending on X,Y∈R. At least Mathematica cannot do it.

ShowAd[ad = 2ad[mats = {( {{0, 0, 0}, {0, 0, -1}, {0, 1, 0}} ), ( {{0, 0, 1}, {0, 0, 0}, {-1, 0, 0}} ), ( {{0, -1, 0}, {1, 0, 0}, {0, 0, 0}} )}]]

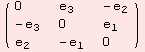
$( {{0, e_3, -e_2}, {-e_3, 0, e_1}, {e_2, -e_1, 0}} )$

The first terms of the Campbell-Baker-Hausdorff series provide a good approximation of the group action, as we show numerically. First, have a look at the coefficients of the series. {,,}{,,}.

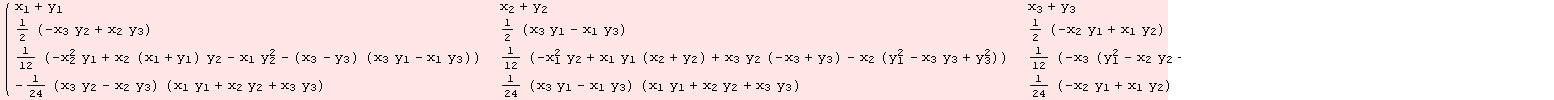
For numerical input as X={-.5,.5,-.5} the command adCBH is much faster than for symbolic input. The plot below visualizes the norm of the difference
|-|
The results are encouraging. When working with R and matrices close to the identity matrix you might as well use the CBH formula to model the group action. By the way, x(-x)=0.

[Graphics:../HTMLFiles/index_390.gif]

Created by Mathematica (September 30, 2006)