Structure equation of Mauer-Catan form

We continue to work with the Lie group SL_2R and its familiar commutator relation.

G = Setup[{(x_1 y_1 + x_2 y_3)/(1 + x_3 y_2), (x_2 + x_1 y_2)/(1 + x_3 y_2), (x_3 y_1 + y_3)/(1 + x_3 y_2)}, {1, 0, 0}] ;

ShowAd[ad = ad[G]]

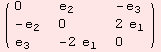
( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} )

In the section on left-invariant tensor fields, we have made implicit use of the following form ω_G:X(G)→g, called Mauer-Catan form. The function of the kernel to compute the form, however, is denoted GdL. This is because ω_G=dL_x^-| _x.

MF[ω = dL[G]]

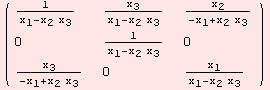
( {{1/(x_1 - x_2 x_3), x_3/(x_1 - x_2 x_3), x_2/(-x_1 + x_2 x_3)}, {0, 1/(x_1 - x_2 x_3), 0}, {x_3/(-x_1 + x_2 x_3), 0, x_1/(x_1 - x_2 x_3)}} )

We would like to check the structure equation dω(X,Y)=-1/2[ω(X),ω(Y)]=-1/2ad.ω.X.ω.Y for all vector fields X,Y∈X(G). The bold "d" denotes the differential on forms. First, we determine dω.

ShowMat[With[{dω = Μd[ω, 1]}, dω - T[dω, {1, 3, 2}]]/2//S]

The next result corresponds to -1/2ad.ω.ω. The two tensors fields are equal.

ShowMat[-T[ad . ω, {1, 3, 2}] . ω/2//S]

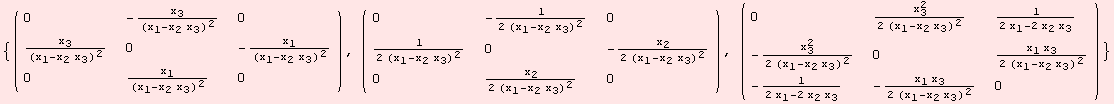
Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!