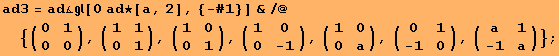
All real 3-dimensional Lie groups
The following list was taken from the paper "Invariants of real low dimension Lie algebras" [Patera et al.].
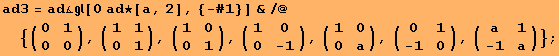
![AppendTo[ad3, Table2ad[({{0, e_1, -2e_2}, {0, 0, e_3}, {0, 0, 0}})]] ;](../HTMLFiles/index_266.gif)
![AppendTo[ad3, Table2ad[({{0, e_3, -e_2}, {0, 0, e_1}, {0, 0, 0}})]] ;](../HTMLFiles/index_267.gif)
The following list summarizes the commutator tables. The coefficient a ranges over special intervals. First 0<a<1, secondly 0<a.
![]()
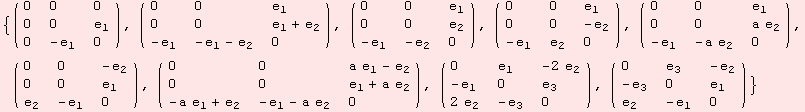
The first 7 Lie algebras in the list are semi-direct products determined by a certain derivation δ. The groups are all diffeomorphic to ![]() . We list the actions G×G→G in coordinates.
. We list the actions G×G→G in coordinates.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The computer determines the group action by exponentiating δ. The derivation δ is part of the commutator table.
![]()
![]()
Lets show all figures that come with Lie algebra #7.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![( {{^(-a x_3) Cos[x_3], -^(-a x_3) Sin[x_3], 0}, {^(-a x_3) Sin[x_3], ^(-a x_3) Cos[x_3], 0}, {0, 0, 1}} )](../HTMLFiles/index_295.gif) |
![( {{^(-a x_3) Cos[x_3], -^(-a x_3) Sin[x_3], a x_1 + x_2}, {^(-a x_3) Sin[x_3], ^(-a x_3) Cos[x_3], -x_1 + a x_2}, {0, 0, 1}} )](../HTMLFiles/index_296.gif) |
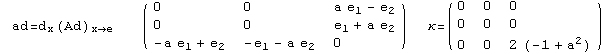
The last two algebras are simple. Lie algebra #8 is ![]() R and is treated in the introduction. Lie algebra #9 is
R and is treated in the introduction. Lie algebra #9 is ![]() R and treated in a separate section. So far, we have ommitted the 3-dimensional abelian group. Lets state a non trivial action
R and treated in a separate section. So far, we have ommitted the 3-dimensional abelian group. Lets state a non trivial action ![]() ×
×![]() →
→![]() as follows
as follows
![]()
![]()
![]()
![]()
![]()
![]()
![]()
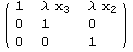 |
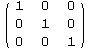 |
| 1 | 1 |
![]()
| Created by Mathematica (September 30, 2006) |