docu5_lie-groups.nb

Two dimensional non-abelian groups

1. Semi-direct product, neutral element at {0,0}. Let the group action G×G→G in coordinates be (,)◦(,)={+ ,+}. In debug-mode the function ShowG lists all relevant figures:
- the inverse mapping, which is computed from the group action and neutral element
- the differential :G→G
- the ad tensor of the corresponding Lie algebra and its killing form.

$Show[2s = Setup[{x_1 + ^(-x_2) y_1, x_2 + y_2}]] ;$

$eqs: ^x_2≠0&&y_1 == -^x_2 x_1&&y_2 == -x_2 {{-^x_2 x_1, -x_2}}$

$act {x_1 + ^(-x_2) y_1, x_2 + y_2}$

$inv {-^x_2 x_1, -x_2}$


$( {{^(-x_2), 0}, {0, 1}} )$	$( {{^(-x_2), x_1}, {0, 1}} )$

$ad=d (Ad) ( {{0, e_1}, {-e_1, 0}} ) κ= ( {{0, 0}, {0, 1}} ) x x→e$

For instance, you will discover ad in the list as

$( {{0, e_1}, {-e_1, 0}} )$

This group action is the result of the semidirect product between two one-dimensional (abelian) groups. In such a scenario, the function adδ reverse-engineers the group action.

${{x_1 + ^(-x_2) y_1, x_2 + y_2}, {0, 0}, {-^x_2 x_1, -x_2}}$

Note, that the output also gives e and the inverse element computation. In combination with GSetup, adδ is a powerful tool:

${x_1 + ^(-x_2) y_1, x_2 + y_2}$

2. Affine group, neutral element at {1,0}. The next group action - however isomorphic - is motivated by the action of the following linear group. Let us assume 0<.

$A = ({{x_1, x_2}, {0, 1}}) ;$

$( {{x_1 y_1, x_2 + x_1 y_2}, {0, 1}} )$

We combine the result and assign e={1,0} as neutral element.

$Show[2a = Setup[{x_1 y_1, x_2 + x_1 y_2}, {1, 0}]] ;$

$eqs: x_1≠0&&y_1 == 1/x_1&&y_2 == -x_2 y_1 {{1/x_1, -x_2/x_1}}$

$act {x_1 y_1, x_2 + x_1 y_2}$

$inv {1/x_1, -x_2/x_1}$


$( {{x_1, 0}, {0, x_1}} )$	$( {{1, 0}, {-x_2, x_1}} )$

$ad=d (Ad) ( {{0, e_2}, {-e_2, 0}} ) κ= ( {{1, 0}, {0, 0}} ) x x→e$

3. Duisenmaat/Kolk group, neutral element at {1,0}. The group action found in Duisenmaat/Kolk is motivated by the action of the following linear group. Again, we assume 0<.

$A = ({{x_1, x_2}, {0, 1/x_1}}) ;$

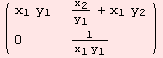
$( {{x_1 y_1, x_2/y_1 + x_1 y_2}, {0, 1/(x_1 y_1)}} )$

We combine the values and assign e={1,0} as neutral element.

$Show[2d = Setup[{x_1 y_1, x_2/y_1 + x_1 y_2}, {1, 0}]]$

$eqs: x_1≠0&&y_1 == 1/x_1&&y_2 == -x_2 {{1/x_1, -x_2}}$

$act {x_1 y_1, x_2/y_1 + x_1 y_2}$

$inv {1/x_1, -x_2}$


$( {{x_1, 0}, {-x_2, x_1}} )$	$( {{1, 0}, {-2 x_1 x_2, x_1^2}} )$

$ad=d (Ad) ( {{0, 2 e_2}, {-2 e_2, 0}} ) κ= ( {{4, 0}, {0, 0}} ) x x→e$

Comparison: Lets recall the three different actions:

${x_1 + ^(-x_2) y_1, x_2 + y_2}$

${x_1 y_1, x_2 + x_1 y_2}$

${x_1 y_1, x_2/y_1 + x_1 y_2}$

The left-invariant vector fields are closed under the commutator operation. They form a finite-dimensional vector space, which is represented by the Lie algebra g. Have a look at the different "bases" here.