Left-invariant geometry

We continue with discussion of the Lie group SL_2R. A group G equipped with a left-invariant metric g becomes a very special semi-Riemannian manifold (G,g).

G = Setup[{(x_1 y_1 + x_2 y_3)/(1 + x_3 y_2), (x_2 + x_1 y_2)/(1 + x_3 y_2), (x_3 y_1 + y_3)/(1 + x_3 y_2)}, {1, 0, 0}] ;

In the section on left-invariant tensor fields, we described how a scalarproduct B on T_eG translates to a left-invariant metric g. The example given is the left matrix below. To the right, we show the right-invariant metric.

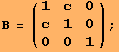
B = ({{1, c, 0}, {c, 1, 0}, {0, 0, 1}}) ;

{ℊ = ΤL[G, B, 0], ΤR[G, B, 0]}//ShowMat

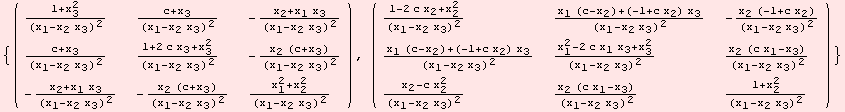
We demand c∉{-1,1}, since

Det[B]

1 - c^2

As a semi-Riemannian manifold (G,g) the geometric tensors such as R and Ric compute by the well known formulas. In our case we have the coordinates {x_1,x_2,x_3}. For instance, the Ricci curvature tensor field is of the form:

showMe = "Ric" ; ShowΜ[ℊ] ;

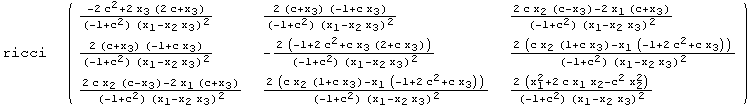
The Ricci curvature tensor field evaluated at e∈G denoted by Ric_0, defines a symmetric bilinear on T_eG. As we show below, Ric is just the induced left-invariant (0,2)-tensor field of the bilinear form Ric_0.

MF[ric0 = ΜRic[ℊ] ◦G[0]//Expand//S]

MF[ΤL[G, ric0, 0]//Expand//S]

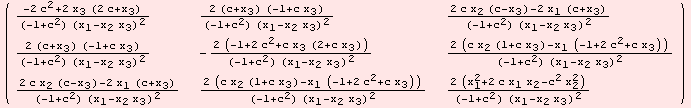
For all geometric tensors, there are formulas in terms of ad and B, which are tensors in T_eG. However, Lie-groups are special homogeneous spaces. At this point of the documentation, we only give a brief motivation of what the code can do. First, we recall the ad tensor.

ShowAd[ad = ad[G]]

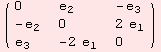
( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} )

The function ShowΗ provides us with ℛ_0 and Ric_0.

showMe = "ℛ,Ric" ; ShowΗ[ad, B] ;

fine:

ℛ_ (1, 2, j)^i ℛ_ (1, 3, j)^i ℛ_ (2, 3, j)^i
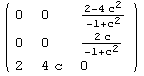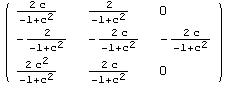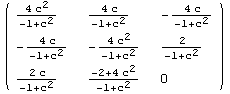( {{0, 0, (2 - 4 c^2)/(-1 + c^2)}, {0, 0, (2 c)/(-1 + c^2)}, {2, 4 c, 0}} ) ( {{(2 c)/(-1 + c^2), 2/(-1 + c^2), 0}, {-2/(-1 + c^2), -(2 c)/(-1 + c^2), -(2 c)/(-1 + c^2)}, {(2 c^2)/(-1 + c^2), (2 c)/(-1 + c^2), 0}} ) ( {{(4 c^2)/(-1 + c^2), (4 c)/(-1 + c^2), -(4 c)/(-1 + c^2)}, {-(4 c)/(-1 + c^2), -(4 c^2)/(-1 + c^2), 2/(-1 + c^2)}, {(2 c)/(-1 + c^2), (-2 + 4 c^2)/(-1 + c^2), 0}} )

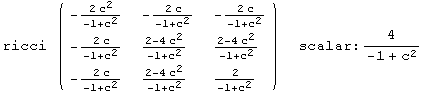
Note, that also the Riemannian curvature coincides.

Showℛ[Μℛ[ℊ] ◦G[0]]

ℛ_ (1, 2, j)^i ℛ_ (1, 3, j)^i ℛ_ (2, 3, j)^i
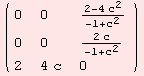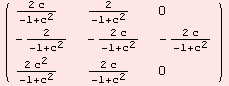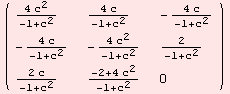( {{0, 0, (2 - 4 c^2)/(-1 + c^2)}, {0, 0, (2 c)/(-1 + c^2)}, {2, 4 c, 0}} ) ( {{(2 c)/(-1 + c^2), 2/(-1 + c^2), 0}, {-2/(-1 + c^2), -(2 c)/(-1 + c^2), -(2 c)/(-1 + c^2)}, {(2 c^2)/(-1 + c^2), (2 c)/(-1 + c^2), 0}} ) ( {{(4 c^2)/(-1 + c^2), (4 c)/(-1 + c^2), -(4 c)/(-1 + c^2)}, {-(4 c)/(-1 + c^2), -(4 c^2)/(-1 + c^2), 2/(-1 + c^2)}, {(2 c)/(-1 + c^2), (-2 + 4 c^2)/(-1 + c^2), 0}} )
Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!