Left-invariant tensor fields

We work with the Lie group defined in the previous section.

G = Setup[{(x_1 y_1 + x_2 y_3)/(1 + x_3 y_2), (x_2 + x_1 y_2)/(1 + x_3 y_2), (x_3 y_1 + y_3)/(1 + x_3 y_2)}, {1, 0, 0}] ;

We confirm that the Lie algebra of our group G is determined by the commutator

ShowAd[ad = ad[G]]

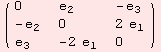
( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} )

Denote with e_i∈T_eG the canonical basis vectors for the tangent space T_eG. e_i generates a left-invariant Killing vector field on G. Locally the vector fields induced by e_1 and e_2 are

X1 = ΤL[G, {1, 0, 0}, 1]

X2 = ΤL[G, {0, 1, 0}, 1]

ΜCom[X1, X2]

{x_1, 0, x_3}

{-x_1 x_3, x_1 - x_2 x_3, -x_3^2}

{-x_1 x_3, x_1 - x_2 x_3, -x_3^2}

Because [X_1,X_2]=X_2, we have just confirmed the entry [e_1,e_2]=e_2 in ad commutator table above!

e1 = {1, 0, 0} ;

e2 = {0, 1, 0} ;

ad . e1 . e2

{0, 1, 0}

Note, the function GTL transforms a tensor of arbitrary rank to a left-invariant tensor field. The integer r, which denotes the rank of the (r,s)-tensor, is made input to the function GTL as well. So, what is behind GTL?

? ΤL

Global`GΤL

GΤL[G_,X_,r_Integer]:=S[Τα[X,r,GdL[G]]]

GTL is just a change of basis! In order to compute the (r,s)-tensor with respect to the new basis, it uses the command Τα. The basis transformation is determined by GdL and depends the coordinates {x_1,x_2,x_3}.

MF[dL[G]]

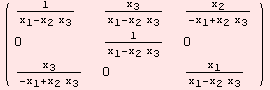
( {{1/(x_1 - x_2 x_3), x_3/(x_1 - x_2 x_3), x_2/(-x_1 + x_2 x_3)}, {0, 1/(x_1 - x_2 x_3), 0}, {x_3/(-x_1 + x_2 x_3), 0, x_1/(x_1 - x_2 x_3)}} )

To obtain a left-invariant metric, i.e. a (0,2)-tensor field with special properties, we apply GΤL to a scalarproduct on T_eG. Recall, a scalar product is a (0,2)-tensor. As a bilinear form, let the scalar product be defined by the symmetric matric B with respect to the canonic basis.

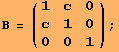
B = ({{1, c, 0}, {c, 1, 0}, {0, 0, 1}}) ;

Det[B]

1 - c^2

Remember, this is only an example. Any other symmetric matric with det≠0, will do. We show the resulting metric g, and the metric, scaled by the common denominator.

{ℊ = ΤL[G, B, 0], ℊ (x_1 - x_2 x_3)^2}//S//ShowMat

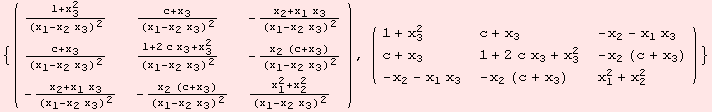
To check, that the metric is indeed left-invariant, we simple input the left-invariant vector field we have yielded above. The outcome is constant and equals the generating vectors scalar producted by B.

ℊ . X1 . X2 == B . {1, 0, 0} . {0, 1, 0}//S

True

What is the left-invariant (1,2)-tensor field Overscript[ad, _] induced by the (1,2)-tensor ad? GΤL gives the answer. The Jacobi identity is satisfied at any coordinate point.

ShowAd[adf = ΤL[G, ad, 1]//S]

E0[adJacobi[adf]]

{True}

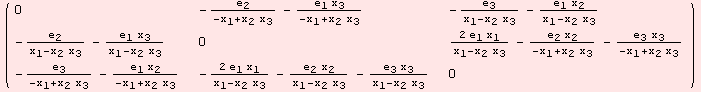
Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!