Defining a Lie group

We input the action and the coordinates of the neutral element derived in the previous section to the function GSetup. The output of GSetup is a function pointer G, which gives us access to the Lie group. From the previous section, we know the following group action coincides locally to SL_2R.

G = Setup[{(x_1 y_1 + x_2 y_3)/(1 + x_3 y_2), (x_2 + x_1 y_2)/(1 + x_3 y_2), (x_3 y_1 + y_3)/(1 + x_3 y_2)}, {1, 0, 0}] ;

The command Gad computes the corresponding Lie algebra commutator tensor ad. Indeed, ad coincides with the matrix commutator for matrices X with trace X=0.

{ShowAd[ad[G]], ShowAd[2ad[{1/2 ( {{1, 0}, {0, -1}} ), ( {{0, 1}, {0, 0}} ), ( {{0, 0}, {1, 0}} )}], 0]}

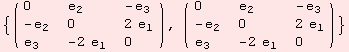
{( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} ), ( {{0, e_2, -e_3}, {-e_2, 0, 2 e_1}, {e_3, -2 e_1, 0}} )}

But back to the group. To perform the group operation g◦h between two elements g,h∈G, lots of notation is allowed. A few examples are

G[g, h]

G[{a, x_1, x_2}, h]

{(g_1 h_1 + g_2 h_3)/(1 + g_3 h_2), (g_2 + g_1 h_2)/(1 + g_3 h_2), (g_3 h_1 + h_3)/(1 + g_3 h_2)}

{(a h_1 + h_3 x_1)/(1 + h_2 x_2), (a h_2 + x_1)/(1 + h_2 x_2), (h_3 + h_1 x_2)/(1 + h_2 x_2)}

The neutral element leaves any element fix. Numerical values are allowed - of course.

G[{1, 0, 0}, {h_1, h_2, h_3}]

G[{1, 2/3, 3/5}, {1/2, 5/6, 1}]

{h_1, h_2, h_3}

{7/9, 1, 13/15}

By the way, the neutral element is stored as

G[0]

{1, 0, 0}

The inverse mapping is restored by

G[x]

G[{a, x_1, x_2}]

{1/x_1, -x_2/x_1, -x_3/x_1}

{1/a, -x_1/a, -x_2/a}

Input vectors have to be of length equal to the dimension of the group. In our case dim G=3.

G[]

3

So the following input causes an error.

G[{x_1}, h]

Setup :: Dimensions : violation in group action

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!