Solvability, Cartans criterion

Next comes the algebra of upper triangular 3×3 matrices.

ShowMat[mats = Algebra[3, inv]]

ShowAd[ad = 2ad[mats]]

( {{0, e_2, e_3, 0, 0, 0}, {-e_2, 0, 0, e_2, e_3, 0}, {-e_3, 0, 0, 0, 0, e_3}, {0, -e_2, 0, 0, e_5, 0}, {0, -e_3, 0, -e_5, 0, e_5}, {0, 0, -e_3, 0, -e_5, 0}} )

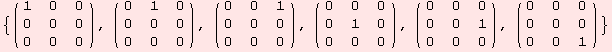
By the way, invt as shown below, encodes the linear condition for a matrix to have no entries below the diagonal. It is universal for any dimension. Pr is a substitution for PadRight.

? inv

Global`invt

invt={Table[Pr[#1[[k]],k-1],{k,ℓ[#1]}]&}

The 6-dimensional Lie algebra is solvable.

ShowMat[des = adDerived[ad]]

ShowMat[#1 . mats&/@des[[2]]]

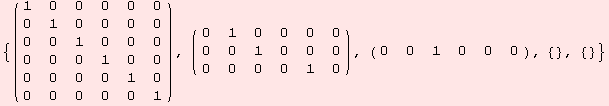
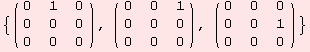
{( {{0, 1, 0}, {0, 0, 0}, {0, 0, 0}} ), ( {{0, 0, 1}, {0, 0, 0}, {0, 0, 0}} ), ( {{0, 0, 0}, {0, 0, 1}, {0, 0, 0}} )}

We recall the following criterion for solvability:
    g is solvable ⇔ κ| _ (×)≡0 for h=[g,g].

MF[κ = adKilling[ad]]

MF[ = des[[2]]]

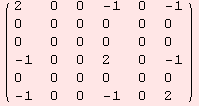
( {{2, 0, 0, -1, 0, -1}, {0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0}, {-1, 0, 0, 2, 0, -1}, {0, 0, 0, 0, 0, 0}, {-1, 0, 0, -1, 0, 2}} )

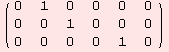
( {{0, 1, 0, 0, 0, 0}, {0, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 1, 0}} )

We can already tell κ| _ (×)≡0 from the figures, however

MF[ . κ . T[]]

zero…3×3

Cartan criterion states: For a subalgebra g⊂_n(R) the following implication holds:
    Tr(X.Y)=0 for all matrices X,Y∈g ⇒ g is solvable.
Lets see, if this criterion applies to the above matrix algebra, with the following basis.

ShowMat[mats]

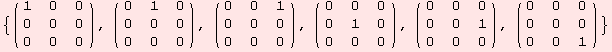
Obviously, this criterion is a joke.

MF[ΤC[ΤC[mats⊗mats, 3, 5], 2, 4]]

( {{1, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0}, {0, 0, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 1}} )

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!