Stabilisator algebras

Stabilisator groups and algebras are perhaps the most important concept in the theory of Lie groups and algebras. The command glAlgebra is the key command to determine a stabilisator algebra, which is considered to be a subalgebra of R or C.
glAlgebra returns a basis of the vector space of matrices determined by a set of linear equations. The equations have to be linear in the coefficients of the matrices.
In the following example, we lists upper-triangular matrices with trace 0.

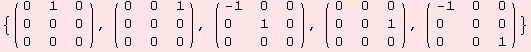
An element X of the algebra could be of the form below. Since we have enforced Tr X=0 and X upper triangular, we guarantee g=exp X has determinant 1 and is upper triangular.

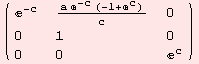
We remark that invt is defined by DGkernel as

The next line produces a subalgebra of R with entry =0. The function that you would like to annihilate is #1[[2,1]]&

The equations you set up, should determine a subspace of matrices that is closed under the bracket operation. If you are not sure, apply glClose afterwards!

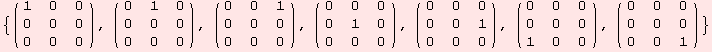
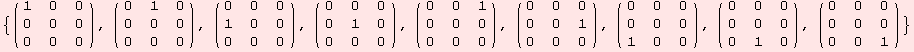
glAlgebra can determine a basis of the Lie algebra of the vectorspace isomorphisms exp X that leave a given (r,s)-tensor A invariant. The strategy is to solve Τdα[A,r,X]=0 to guarantee Τα[A,r,g]=A with g=exp X. If the rank is r=0 and A is a symmetric bilinear form this corresponds to the familiar constellation
    .A+A.X=0 leads to .A.g=A.
Note, .A+A.X=0 is linear in the coefficients of X. Lets produce the matrices for so(2,1).

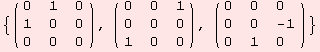
The stabilisator algebra is determined by gl2ad.

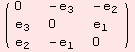
The stabilisator algebra is simple. The killing form is non-degenerated. The set of derivations of an algebra g determined by ad is the Lie algebra of the stabilizator Lie group of ad. We confirm, that all derivations are inner derivations by determining the Lie algebra of the stabilizator Lie group of ad. The dimension of the vector space of inner derivations equals the dimension of the algebra, which is 3. This matches the dimension of the matrix algebra derived by the last command line. Thus all derivations are inner derivations.

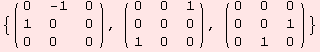
DKkernel features the standard equations that are of common interest. Note, that glAlgebra finds matrices over R or C.

Lets spend the remaing part of the section, to pace through an example of mild complexity. Lets be interested in those transformations g=exp X, that leave the commutator tensor ad of the Heisenberg algebra invariant.

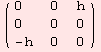
On group level, the equation ad=ad is formulated using Τα. However, the equations are not very pratical to solve.

Instead of determining the matrices of the stabilizer group of the ad tensor, we determine the stabilisator algebra. The function Τdα is the derivative exp t ad.

The list of matrices below shows a basis of the lie algebra of the transformations group we are looking for. We also output its corresponding ad tensor together with Killing-Form.

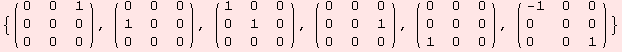
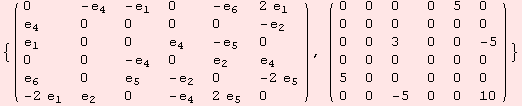
The one-parameter subgroups exp t X where X is an element of the basis of the lie algebra are

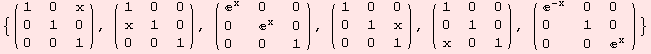
Indeed, basis transformation with any of these matrices - and thus any product thereof - leaves the components of the tensor ad fix.

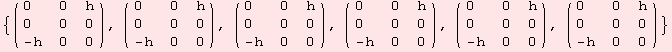
glAlgebra applies to several important applications. The chapter on Homogeneous spaces, pairs and triples features advanced illustrations of the command.

Created by Mathematica  (September 30, 2006)