Close a set of matrices under commutation

glClose takes a set of matrices Σ and generates a basis for a linear algebra, which contains Σ and is closed under the matrix commutator. A few examples are shown below.

ShowMat[Close[{({{0, 1}, {0, 0}}), ({{0, 0}, {1, 0}})}]]

{( {{1, 0}, {0, -1}} ), ( {{0, 1}, {0, 0}} ), ( {{0, 0}, {1, 0}} )}

Why not derive the resulting Lie algebra tensor ad afterwards.

ShowMat[Σclosed = Close[{({{0, 0, 1}, {0, 0, 1}, {1, 0, 0}}), ({{0, 0, 0}, {0, 0, 0}, {1, 0, 0}})}]]

ShowAd[2ad[Σclosed]]

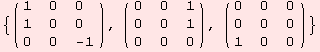
{( {{1, 0, 0}, {1, 0, 0}, {0, 0, -1}} ), ( {{0, 0, 1}, {0, 0, 1}, {0, 0, 0}} ), ( {{0, 0, 0}, {0, 0, 0}, {1, 0, 0}} )}

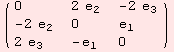
( {{0, 2 e_2, -2 e_3}, {-2 e_2, 0, e_1}, {2 e_3, -e_1, 0}} )

Two final examples:

ShowMat[Σclosed = Close[{({{0, 0, 1}, {1, 0, 1}, {0, 0, 0}}), ({{0, 0, 0}, {0, 1, 0}, {0, 0, 0}})}]]

ShowAd[2ad[Σclosed]]

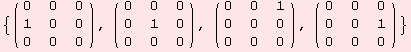
{( {{0, 0, 0}, {1, 0, 0}, {0, 0, 0}} ), ( {{0, 0, 0}, {0, 1, 0}, {0, 0, 0}} ), ( {{0, 0, 1}, {0, 0, 0}, {0, 0, 0}} ), ( {{0, 0, 0}, {0, 0, 1}, {0, 0, 0}} )}

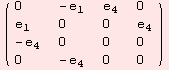
( {{0, -e_1, e_4, 0}, {e_1, 0, 0, e_4}, {-e_4, 0, 0, 0}, {0, -e_4, 0, 0}} )

... and ...

ShowMat[Σclosed = Close[{({{0, 1, 1}, {1, 0, 1}, {0, 0, 0}}), ({{0, 0, 0}, {0, 1, 0}, {0, 0, 0}})}]]

ShowAd[2ad[Σclosed]]

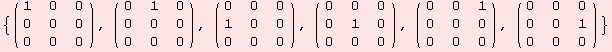
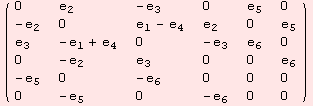
( {{0, e_2, -e_3, 0, e_5, 0}, {-e_2, 0, e_1 - e_4, e_2, 0, e_5}, {e_3, -e_1 + e_4, 0, -e_3, e_6, 0}, {0, -e_2, e_3, 0, 0, e_6}, {-e_5, 0, -e_6, 0, 0, 0}, {0, -e_5, 0, -e_6, 0, 0}} )

... done.

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!