Rootsystems of semi-simple Lie algebras
Let us investigate some simple Lie algebras. First, we consider Lie algebras of type ![]() . In particular
. In particular ![]() and
and ![]() .
.
![]()
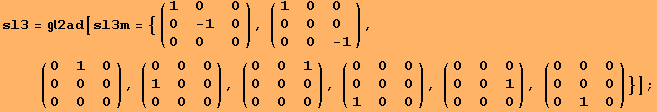
The characteristic polynomial to a Lie algebra is defined as ![]() (λ)=|ad.x-λ Id|.
(λ)=|ad.x-λ Id|.
![]()
![]()
![]()
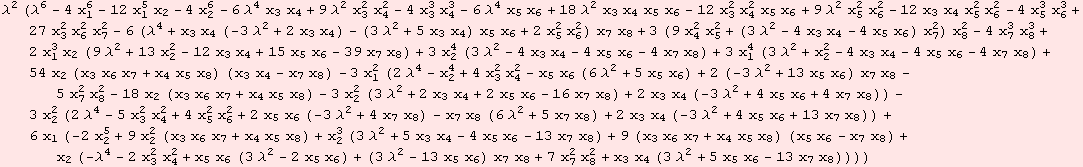
We list the coefficients with respect to the monomials ![]() ,
,![]() ,...,
,...,![]() .
.
![]()
![]()


The number of leading zeros in the coefficient list is the rank of the algebra.
![]()
![]()
![]()
![]()
To determine the roots ![]() , we first need a Cartan subalgebra in our Lie algebra. A Cartan subalgebra is generated by a regular element X∈g.
, we first need a Cartan subalgebra in our Lie algebra. A Cartan subalgebra is generated by a regular element X∈g.
![]()
![]()
In the case of ![]() , an element X={
, an element X={![]() ,
,![]() ,
,![]() }∈
}∈![]() is regular whenever
is regular whenever ![]() +
+![]()
![]() ≠0. The dimension of the eigenspace of a regular X equals the rank of the algebra. Example: {1,0,0} is regular, but {0,1,0} is not.
≠0. The dimension of the eigenspace of a regular X equals the rank of the algebra. Example: {1,0,0} is regular, but {0,1,0} is not.
![]()
![]()
![]()
![]()
![]()
![]()
Any regular element suits to generate a Cartan subalgebra. In the first iteration, lets fix ![]() =<{
=<{![]() ,0,0}> as the 1-dimensional Cartan subalgebra denoted
,0,0}> as the 1-dimensional Cartan subalgebra denoted ![]() . A root of the simple algebra g is a form α∈
. A root of the simple algebra g is a form α∈![]() with α≠0 so that |ad.H-α.H|=0 for all H∈h.
with α≠0 so that |ad.H-α.H|=0 for all H∈h.
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_166.gif]](../HTMLFiles/index_166.gif)
The root space to a root α≠0 is defined ![]() :={X∈g:X∈ker ad.H-α.H Id}.
:={X∈g:X∈ker ad.H-α.H Id}. ![]() is always 1-dimensional. For semi-simple g, we have the decomposition g=
is always 1-dimensional. For semi-simple g, we have the decomposition g=![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
To determine the roots and the rootspaces, the functions require the cartan subalgebra to be spanned by the first, i.e. leading basis elements. Say you would like to choose the Cartan algebra ![]() different from above, maybe as
different from above, maybe as
![]()
![]()
We basis transform the ad-tensor so that {1,1,1} is the first basis element, and then run the same code.
![]()
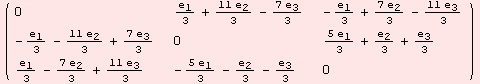
![]()
![]()
![]()
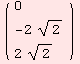
![[Graphics:../HTMLFiles/index_185.gif]](../HTMLFiles/index_185.gif)
![]()
![]()
![]()
There is the notion of normed star vectors, but the implementation might be erroneous. The normed star vectors in both cases should have at least the same lenght.
![]()
![]()
![]()
![]()
A more exciting scenario is that of ![]() . The "canonic" 2-dimensional Cartan subalgebra is that of the diagonal matrices.
. The "canonic" 2-dimensional Cartan subalgebra is that of the diagonal matrices.
![]()
![]()
![]()
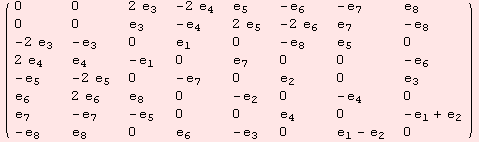
The command adRoots involves the computation of the rank of the algebra.
![]()
![]()
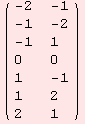
![[Graphics:../HTMLFiles/index_201.gif]](../HTMLFiles/index_201.gif)
A different choice of the Cartan subalgebra is, for instance, given by
![]()
![]()
![]()
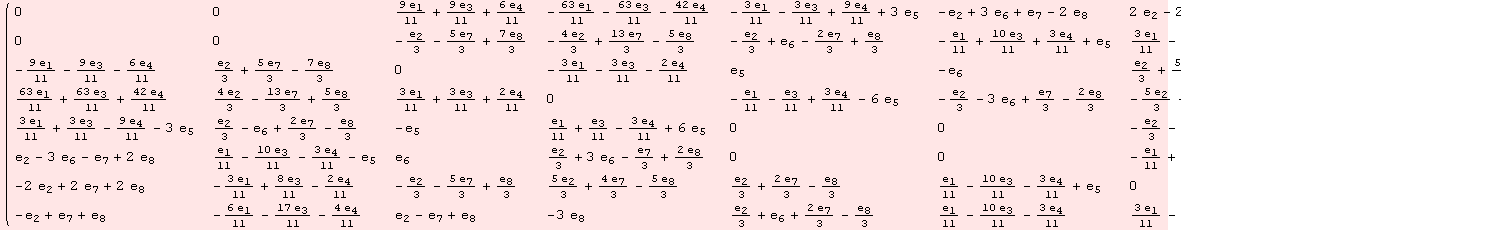
The ad tensor has been transformed, so that the abelian subalgebra is spanned by ![]() ,
,![]() . The coordinates of the roots have altered.
. The coordinates of the roots have altered.
![]()
![]()
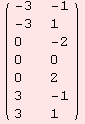
![[Graphics:../HTMLFiles/index_211.gif]](../HTMLFiles/index_211.gif)
Finally, we confirm the decomposition g=![]()
![]()
![]() in both cases.
in both cases.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
star vectors
![]()
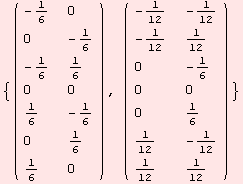
Again, the normed star vectors are probably erroneous.
![]()
![]()
![[Graphics:../HTMLFiles/index_235.gif]](../HTMLFiles/index_235.gif)
![[Graphics:../HTMLFiles/index_236.gif]](../HTMLFiles/index_236.gif)
Finally, let us investigate ![]() . Note, the characteristic polynomial below as
. Note, the characteristic polynomial below as ![]() (λ)=|ad.x-λ Id|.
(λ)=|ad.x-λ Id|.
![]()
![]()
![]()
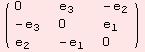
![]()
We list the coefficients with respect to the monomials ![]() ,
,![]() ,...,
,...,![]() . The number of leading zeros in the coefficient list is the rank of the algebra.
. The number of leading zeros in the coefficient list is the rank of the algebra.
![]()
![]()
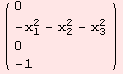
![]()
To determine the roots ![]() , we first need a Cartan subalgebra in our Lie algebra. A Cartan subalgebra is generated by a regular element X∈g.
, we first need a Cartan subalgebra in our Lie algebra. A Cartan subalgebra is generated by a regular element X∈g.
![]()
![]()
In the case of ![]() , an element X={
, an element X={![]() ,
,![]() ,
,![]() }∈
}∈![]() is regular whenever
is regular whenever ![]() +
+![]() +
+![]() ≠0. The dimension of the eigenspace of a regular X equals the rank of the algebra. Thus, non-regular elements X≠0 have complex entries, such as X={i,1,0}.
≠0. The dimension of the eigenspace of a regular X equals the rank of the algebra. Thus, non-regular elements X≠0 have complex entries, such as X={i,1,0}.
![]()
![]()
![]()
![]()
Lets fix ![]() =<{
=<{![]() ,0,0}> as the 1-dimensional Cartan subalgebra denoted
,0,0}> as the 1-dimensional Cartan subalgebra denoted ![]() . A root of the simple algebra g is a form α∈
. A root of the simple algebra g is a form α∈![]() with α≠0 so that |ad.H-α.H|=0 for all H∈h. The root space to a root α≠0 is defined
with α≠0 so that |ad.H-α.H|=0 for all H∈h. The root space to a root α≠0 is defined ![]() :={X∈g:X∈ker ad.H-α.H Id}.
:={X∈g:X∈ker ad.H-α.H Id}. ![]() is always 1-dimensional. For semi-simple g, we have the decomposition g=
is always 1-dimensional. For semi-simple g, we have the decomposition g=![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_279.gif]](../HTMLFiles/index_279.gif)
![]()
![]()
![]()
| Created by Mathematica (September 30, 2006) |