Killing form

The command adKilling takes as input an ad tensor and outputs the killing form κ, which is a bilinear form.

ShowAd[ad = Table2ad[({{0, 0, e_1 + e_2}, {0, 0, e_2}, {-e_1 - e_2, -e_2, 0}})]]

MF[adKilling[ad]]

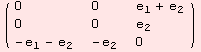
( {{0, 0, e_1 + e_2}, {0, 0, e_2}, {-e_1 - e_2, -e_2, 0}} )

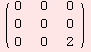
( {{0, 0, 0}, {0, 0, 0}, {0, 0, 2}} )

The computation of κ is fairly simple. κ is a contraction of the (1,3)-tensor ad.ad. Have a look at the code:

? adKilling

Global`adKilling

adKilling[ad_]:=ΤC[ad.ad,1,4]

If κ is non-degenerated, i.e. det(κ)≠0, the algebra is semi-simple. The next examples are taken from [HN91] on p.108 and p.124. Below, we are dealing with sl(2,R).

ShowAd[ad = 2ad[{({{1, 0}, {0, -1}}), ({{0, 1}, {-1, 0}}), ({{0, 1}, {1, 0}})}]]

adKilling[ad]//MF

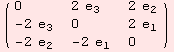
( {{0, 2 e_3, 2 e_2}, {-2 e_3, 0, 2 e_1}, {-2 e_2, -2 e_1, 0}} )

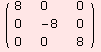
( {{8, 0, 0}, {0, -8, 0}, {0, 0, 8}} )

Here comes the treatment of so(3):

ShowAd[ad = 2ad[Algebra[3, inv[3], ]]]

adKilling[ad]//MF

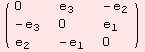
( {{0, e_3, -e_2}, {-e_3, 0, e_1}, {e_2, -e_1, 0}} )

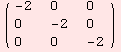
( {{-2, 0, 0}, {0, -2, 0}, {0, 0, -2}} )

Both algebras are semi-simple (moreover simple), because the Killing form is non-degenerated.

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!