Descending series, derived series

Consider the 2-dimensional non-abelian algebra of the following group action G×G→G with {x_1,x_2}◦{y_1,y_2}={x_1+^(-x_2) y_1,x_2+y_2}.

ShowAd[ad = ad[Setup[{x_1 + ^(-x_2) y_1, x_2 + y_2}]]]

( {{0, e_1}, {-e_1, 0}} )

The algebra is not nilpotent, ...

ShowMat[adDescend[ad]]

{( {{1, 0}, {0, 1}} ), ( {{1, 0}} ), ( {{1, 0}} )}

... but solvable.

ShowMat[adDerived[ad]]

{( {{1, 0}, {0, 1}} ), ( {{1, 0}} ), {}, {}}

An example of a nilpotent (⇒ solvable) 5-dimensional algebra.

ad = Table2ad[{h, p_1, p_2, q_1, q_2}, ({{0, 0, 0, p_1, p_2}, {0, 0, 0, 0, 0}, {0, 0, 0, 0, 0}, {-p_1, 0, 0, 0, h}, {-p_2, 0, 0, -h, 0}})] ;

ShowMat[adDescend[ad]]

ShowMat[adDerived[ad]]

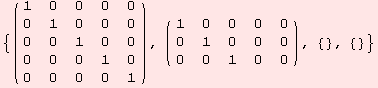
{( {{1, 0, 0, 0, 0}, {0, 1, 0, 0, 0}, {0, 0, 1, 0, 0}, {0, 0, 0, 1, 0}, {0, 0, 0, 0, 1}} ), ( {{1, 0, 0, 0, 0}, {0, 1, 0, 0, 0}, {0, 0, 1, 0, 0}} ), {}, {}}

The row vectors in each of these matrices, span the corresponding subspaces like [g,g], or [[g,g],g]. The properties: nilpotency and solvability are independent of the basis.

{MF[α = Array[Random[Integer, {-1, 1}] &, {5, 5}]], Det[α]}

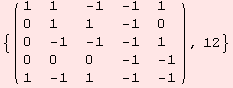
{( {{1, 1, -1, -1, 1}, {0, 1, 1, -1, 0}, {0, -1, -1, -1, 1}, {0, 0, 0, -1, -1}, {1, -1, 1, -1, -1}} ), 12}

But note, with respect to a different basis α, the subspaces like [g,g], or [[g,g],g] transform as well.

ShowAd[adτ = Τα[ad, 1, α]]

ShowMat[adDescend[adτ]]

ShowMat[adDerived[adτ]]

{( {{1, 0, 0, 0, 0}, {0, 1, 0, 0, 0}, {0, 0, 1, 0, 0}, {0, 0, 0, 1, 0}, {0, 0, 0, 0, 1}} ), ( {{1, 0, -1, 0, 0}, {0, 1, 1, 0, 0}, {0, 0, 0, 1, -1}} ), {}, {}}

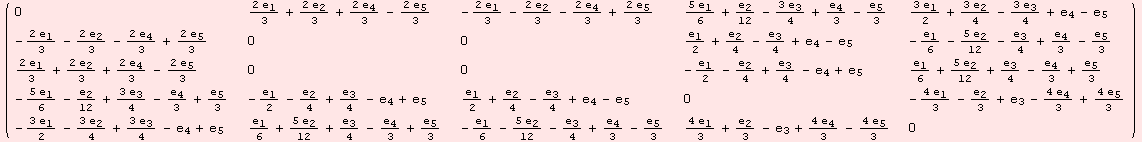
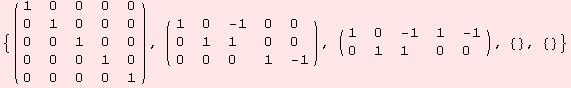
Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!