The simple algebra

The simple Lie group is the stabilizator group of the following (0,3)-tensor ω.

We obtain a basis of the matrix algebra of using the command glAlgebra.

The algebra is 14-dimensional. The commutator tensor with respect to the matrix basis above is

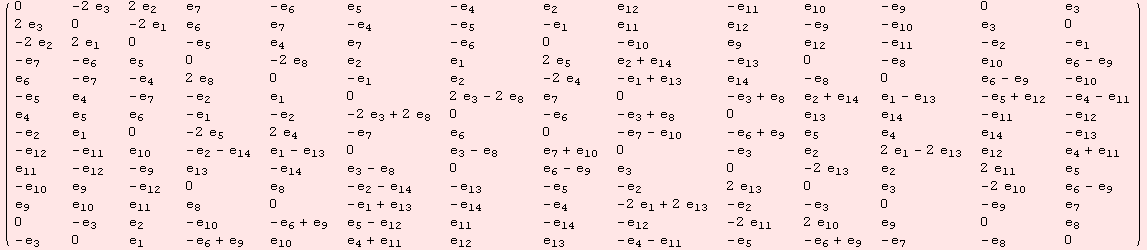
In order to obtain a root system, we obtain a Cartan subalgebra by guessing a regular element. The rank of the algebra is 2, so the element X=+ used below is regular, because the eigenspace of is two dimensional for great values of n.

We transform the basis so that the Cartan subalgebra is spanned by the first two elements.

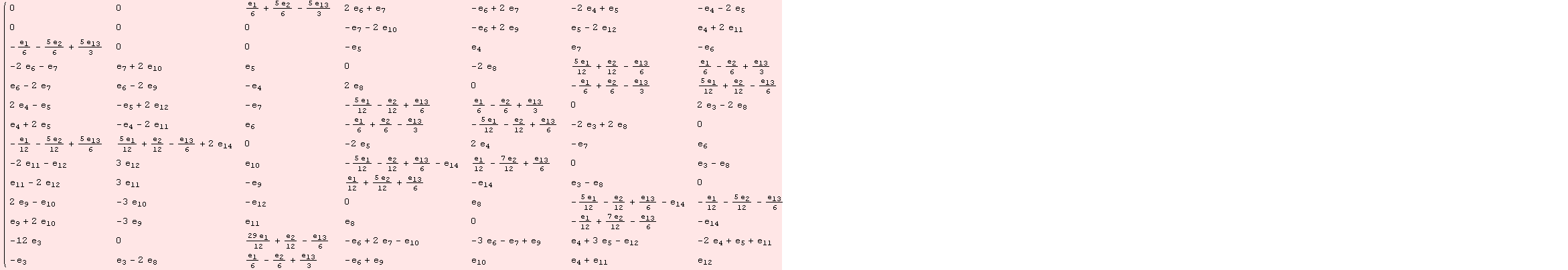
Unfortunately, our implementation is not good enougth to solve for the roots at this point. The characteristic polynomial is too complicated.

Created by Mathematica  (September 30, 2006)