Introduction

A Lie algebra is a vector space together with a special (1,2)-tensor called commutator, or ad tensor. To define a Lie algebra in Mathematica, enter the (1,2)-tensor ad as a skew-symmetric "matrix", using the command Table2ad.

ShowAd[ad = Table2ad[({{0, e_1 + a e_2, e_3}, {-e_1 - a e_2, 0, λ (e_3 + e_1)}, {-e_3, -λ (e_3 + e_1), 0}})]]

not jacobian.

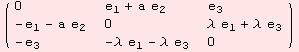
( {{0, e_1 + a e_2, e_3}, {-e_1 - a e_2, 0, λ e_1 + λ e_3}, {-e_3, -λ e_1 - λ e_3, 0}} )

To evaluate the commutator say [e_1+e_2,b·e_3], we type

ad . {1, 1, 0} . {0, 0, b}

{b λ, 0, b (1 + λ)}

We check, if ad is skew and satisfies the Jacobi identity. ad has to annihilate the functions adSkew and adJacobi. It turns out, that only for certain parameters a and λ, ad is a Lie-algebra commutator.

E0[adSkew[ad]]

E0[adJacobi[ad]]

Solve[E0[adJacobi[ad]]]

{True}

{True, 0 == -(1 + a) λ, 0 == (1 + a) λ, 0 == -1 - a λ, 0 == 1 + a λ}

{{λ→1, a→ -1}}

The tensor ad often represents the commutator of a matrix algebra. gl2ad converts a basis of matrices into the corresponding ad tensor of the matrix Lie algebra. In the following example we are dealing with the algebra sl(2,R).

2 = {1/2 ({{1, 0}, {0, -1}}), 1/2^(1/2) ({{0, 1}, {0, 0}}), 1/2^(1/2) ({{0, 0}, {1, 0}})} ;

ShowAd[ad = 2ad[2]]

( {{0, e_2, -e_3}, {-e_2, 0, e_1}, {e_3, -e_1, 0}} )

The matrices of sl2R and ad correspond in the following way.

X = {a, 0, 1} ;

Y = {1, 3, π} ;

ShowMat[{Com[X . 2, Y . 2], ad . X . Y . 2}//S]

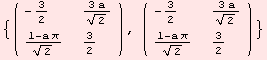
{( {{-3/2, (3 a)/2^(1/2)}, {(1 - a π)/2^(1/2), 3/2}} ), ( {{-3/2, (3 a)/2^(1/2)}, {(1 - a π)/2^(1/2), 3/2}} )}

The following command shows a basis for the smallest subalgebra generated by the set of elements {{0,1,a},{0,1,0}}. The value a is assumed to be non-zero.

adSub[ad, {{0, 1, a}, {0, 1, 0}}]

{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}

The (0,2) tensor Killing-Form of  sl(2,R) in the chosen basis is

B = adKilling[ad] ; B//MF

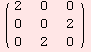
( {{2, 0, 0}, {0, 0, 2}, {0, 2, 0}} )

The α below induces a change of basis, so that Killing-Form is diagonal. The parameter d∈R is arbitrary.

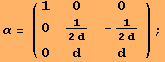
α = ({{1, 0, 0}, {0, 1/(2 d), -1/(2 d)}, {0, d, d}}) ;

ShowMat[{Τα[B, 0, α], T[α] . B . α}]

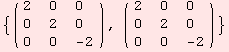
{( {{2, 0, 0}, {0, 2, 0}, {0, 0, -2}} ), ( {{2, 0, 0}, {0, 2, 0}, {0, 0, -2}} )}

As a (1,2) tensor, ad transforms by Τα[ad,1,α]. To carry out these transformations by hand, is a source for  annoying mistakes. Here, a final example:

{ShowAd[ad], adKilling[ad]//MF}

{ShowAd[nad = Τα[ad, 1, α]], adKilling[nad]//MF}

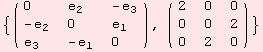
{( {{0, e_2, -e_3}, {-e_2, 0, e_1}, {e_3, -e_1, 0}} ), ( {{2, 0, 0}, {0, 0, 2}, {0, 2, 0}} )}

{( {{0, -e_3, -e_2}, {e_3, 0, e_1}, {e_2, -e_1, 0}} ), ( {{2, 0, 0}, {0, 2, 0}, {0, 0, -2}} )}

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!