Curvature

Thughout this section, we use the unique "Levi-Civita" connection. First, consider the metric defined in the previous section

ℊS3p = ( {{r^2 Cos[x_2]^2 Cos[x_3]^2, 0, 0}, {0, r^2 Cos[x_3]^2, 0}, {0, 0, r^2}} ) ;

In the following, we describe how to obtain the Riemannian curvature (1,3)-tensor field. In fact, the command ΜR does the job.

Showℛ[Μℛ[ℊS3p]]

Rie_ (1, 2, j)^i Rie_ (1, 3, j)^i Rie_ (2, 3, j)^i
( {{0, Cos[x_3]^2, 0}, {-Cos[x_2]^2 Cos[x_3]^2, 0, 0}, {0, 0, 0}} ) ( {{0, 0, 1}, {0, 0, 0}, {-Cos[x_2]^2 Cos[x_3]^2, 0, 0}} ) ( {{0, 0, 0}, {0, 0, 1}, {0, -Cos[x_3]^2, 0}} )

The (0,2)-Ricci curvature tensor field computes as

ΜRic[ℊS3p]//MF

( {{2 Cos[x_2]^2 Cos[x_3]^2, 0, 0}, {0, 2 Cos[x_3]^2, 0}, {0, 0, 2}} )

Many more examples, will follow in later sections. At this place, we point to the feature of using ShowRFunc for more extensive terms.

ShowℛFunc =  ;

Rie_ (1, 2, j)^i
Rie_ (1, 3, j)^i
Rie_ (2, 3, j)^i

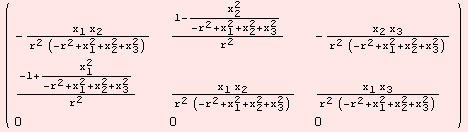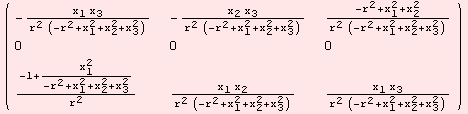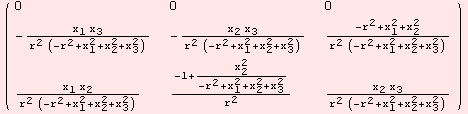... and the Ricci curvature.

MF[ΜRic[ℊ]]

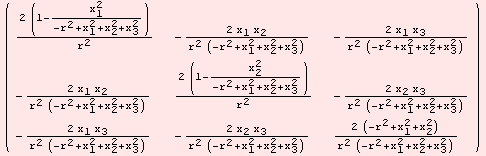
Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!