Geodesics, Exponential Map
Cosider the hyperbolic metric on R×![]() defined for r>0 as
defined for r>0 as
![]()
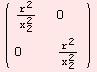
The parameter r does not change the geodesics on R×![]() qualitatively, for r does not appear in the geodesic equations below. Although the expressions for the geodesics are simple, Mathematica has trouble solving the differential equations. Maybe in the next version...
qualitatively, for r does not appear in the geodesic equations below. Although the expressions for the geodesics are simple, Mathematica has trouble solving the differential equations. Maybe in the next version...
![]()
![]()
![]()
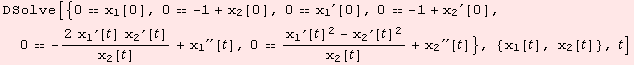
For illustration purposes numerial approximation is good enough. We set r=1, but only for normalization of the initial vector.
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_189.gif]](../HTMLFiles/index_189.gif)
We visualize the function ![]() :
:![]() M→M for p∈M for a particular point p. The lines that appear correspond to the canonical coordinate lines of
M→M for p∈M for a particular point p. The lines that appear correspond to the canonical coordinate lines of ![]() M.
M.
![]()
![[Graphics:../HTMLFiles/index_194.gif]](../HTMLFiles/index_194.gif)
Another example: The following space (M,g) is geodesically complete. However, between two points there might not be a connecting geodesic. M=(![]() ,
,![]() )×R equipped with
)×R equipped with
![]()
![]()
Note that the metric does not depend on the coordinate ![]() .
.

![]()
![]()
![[Graphics:../HTMLFiles/index_203.gif]](../HTMLFiles/index_203.gif)
![[Graphics:../HTMLFiles/index_204.gif]](../HTMLFiles/index_204.gif)
The space is heavily curved near the "boundary"?
![]()
![]()
![[Graphics:../HTMLFiles/index_209.gif]](../HTMLFiles/index_209.gif)
![]()
![]()
Not really. The sectional curvature is constant =1 for non-degenerated planes.
![]()
![]()
![]()
![]()
Finally, the image of the exponential map ![]() for p=(.4,.2) with coordinate lines.
for p=(.4,.2) with coordinate lines.
![]()
![[Graphics:../HTMLFiles/index_218.gif]](../HTMLFiles/index_218.gif)
Next, we consider M=<![]() ,g> with a special Lorentzian metric g. The semi-Riemannian manifold M is not complete, i.e. not all geodesics are defined on the entire real line.
,g> with a special Lorentzian metric g. The semi-Riemannian manifold M is not complete, i.e. not all geodesics are defined on the entire real line.
![]()
![]()
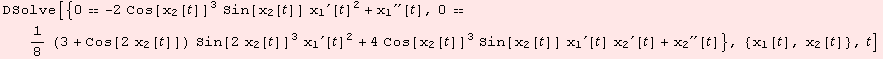
We know, that γ(t)={![]() -t,ArcTan[t]} is a solution. Although, lets check:
-t,ArcTan[t]} is a solution. Although, lets check:
![]()
![]()
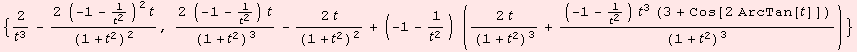
![]()
Everybody can tell what happens for t→0.
![]()
![[Graphics:../HTMLFiles/index_229.gif]](../HTMLFiles/index_229.gif)
Our code does not compensate for this incident.

![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:../HTMLFiles/index_237.gif]](../HTMLFiles/index_237.gif)
| Created by Mathematica (December 22, 2006) |