Christoffel symbols, Levi-Civita connection

The Levi-Civita connection involves the Christoffel (1,2)-tensor field, which is implemented by the command ΜΓ. Assume our metric is that of the geometrical S^3, parametrized in spherical coordinates as

ℊS3p = ( {{r^2 Cos[x_2]^2 Cos[x_3]^2, 0, 0}, {0, r^2 Cos[x_3]^2, 0}, {0, 0, r^2}} ) ;

Then, the Christoffel (1,2)-tensor field is

ShowΓFunc =  ;

ShowΓ[ΜΓ[ℊS3p]]

Choosing slightly different coordinates results in

Γ_ (i, j)^1
Γ_ (i, j)^2
Γ_ (i, j)^3

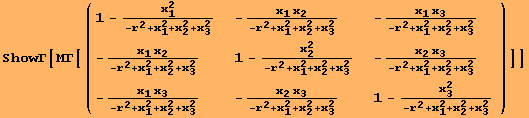
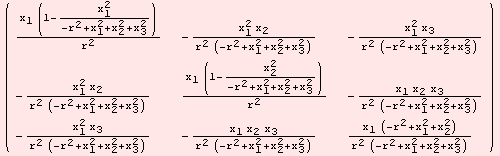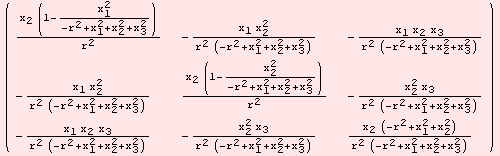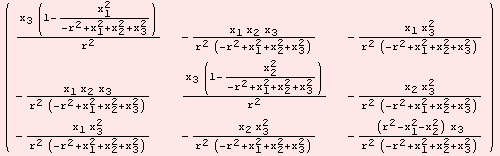The Levi-Civita connection is equivalent to a special covariant derivative, which we implement by Μ▽ in a brief way.

? Μ▽

Global`Μ▽

Μ▽[g_,X_List,r_Integer:1]:=Μd[X,r]+Τdα[X,r,ΜΓ[g]]

The command Μ▽ determines the covariant derivative of tensor fields of arbitrary rank. Below, we compute the covariant derivative of the vector field {x_1,x_2,x_3}. The result is a (1,1)-tensor field.

MF[Μ▽[ℊS3p, {x_1, x_2, x_3}, 1]]

( {{1 - x_2 Tan[x_2] - x_3 Tan[x_3], -x_1 Tan[x_2], -x_1 Tan[x_3]}, {Cos[x_2] Sin[x_2] x_1, 1 - x_3 Tan[x_3], -x_2 Tan[x_3]}, {Cos[x_2]^2 Cos[x_3] Sin[x_3] x_1, Cos[x_3] Sin[x_3] x_2, 1}} )

Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!