Stokes Theorem
We set up a random function to test Stokes theorem.
![]()
![]()
![rpoly := 2Array[rint&, {n, n}] . Τ★[x, n] . Τ★[x, n] + Array[rint&, {n}] . Τ★[x, n] + rint ;](../HTMLFiles/index_484.gif)
![]()
![]()
We scale the operation ΤA(d ◦) by a factor of 2.
![]()
![]()
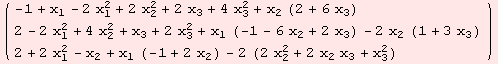
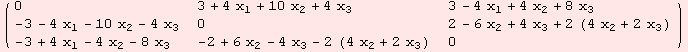
The integrals in question are over ![]() and its boundary. The evaluations coincide.
and its boundary. The evaluations coincide.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The function to be integrated over ![]() is
is
![]()
![]()
The functions on the boundary of ![]() are
are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| Created by Mathematica (December 22, 2006) |