Neukirchner tiling

How many unit discs fit on the torus below? You don't know? We neither.

assum = {0<x_1<2π, 0<x_2<2π, 0<r<R} ;

f = {(R + r Cos[x_2]) Cos[x_1], (R + r Cos[x_2]) Sin[x_1], r Sin[x_2]}/.{R→3.3, r→2.8} ;

pτ = ParametricPlot3D[f, {x_1, 0, 2 π - 1.5}, {x_2, 0, 2π - 1}] ;

[Graphics:../HTMLFiles/index_390.gif]

The command takes care of the numerical oddities that occur:

MF[df = Μd[f, 1, 2]]

MF[ℊ = T[df] . df//Chop//S]

( {{-(3.3 + 2.8 Cos[x_2]) Sin[x_1], -2.8 Cos[x_1] Sin[x_2]}, {Cos[x_1] (3.3 + 2.8 Cos[x_2]), -2.8 Sin[x_1] Sin[x_2]}, {0, 2.8 Cos[x_2]}} )

( {{10.89 + Cos[x_2] (18.48 + 7.84 Cos[x_2]), 0}, {0, 7.84}} )

The figures below are odd, however, they are not oddities.

ShowΓ[ΜΓ[ℊ]]

Γ_ (i, j)^1 Γ_ (i, j)^2
( {{(1. (1.17856 + Cos[x_2]) (1.38904 + Cos[x_2] (2.35715 + Cos[x_2])) Sin[x_2])/((1.17857 + Cos[x_2]) (1.17857 + Cos[x_2])), 0}, {0, 0}} )

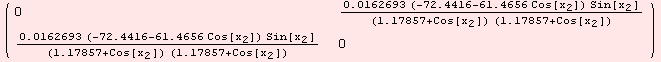Lets write a function that computes (approximately) the border of a unit disc with center at coordinate point p. The function computes an orthonormal frame with respect to ℊ_p. The orthonormal vectors become a basis for T_pM. They provide coordinates on T_pM for the function exp_p:T_pM→M.

p1 = {2.2, 2.8}

mf = disc[p1]

{2.2, 2.8}

{InterpolatingFunction[{{0., 6.28319}}, <>][], InterpolatingFunction[{{0., 6.28319}}, <>][]}

Show[ParametricPlot[Evaluate[disc[p1, #1]], {, 0, 2 π}, DisplayFunction→Identity] &/@Range[3, 10, 2], DisplayFunction→$DisplayFunction] ;

[Graphics:../HTMLFiles/index_411.gif]

In the next figure, we plot a kind of error. We compare boundary curves with sparse resolution to the boundary curves obtained by resolution 20. The resolution is the value n, which is the number of rays we shoot from our disc center p outwards. The error plot indicates that resolution 20 is a safe choice - at least for this point p.

sol = With[{c = disc[p1, #1] - mf}, c . c] &/@Range[7, 12, 2] ;

Plot[Evaluate[sol], {, 0, 2π}] ;

[Graphics:../HTMLFiles/index_414.gif]

Random balls on the torus.

[Graphics:../HTMLFiles/index_416.gif]

Another picture. Disc boundaries are all with distance 1 from center.

[Graphics:../HTMLFiles/index_418.gif]

Let us detect the intersection of to disc which intersect. This is rather a numerical experiment of what Mathematica is able to do.

d1 = disc[{1.1, .8}] ;

d2 = disc[{1.3, 1.2}] ;

[Graphics:../HTMLFiles/index_422.gif]

We take the euclidean distance to obtain a distance function of the curves. The function depends on t and s, which are the parameters for the two curves.

dist = With[{v = (d1 - (d2/.→))}, (v . v)^(1/2)] ;

Plot3D[dist, {, 0, 2π}, {, 0, 2π}, PlotPoints→ {30, 30}] ;

[Graphics:../HTMLFiles/index_425.gif]

Maybe there is a better function in Mathematica for what we are trying to do. Especially, with FindMinimum we can only finds one solution.

{z, β} = FindMinimum[dist, {, π, 0, 2π}, {, π, 0, 2π}]

Show[{pγ, Graphics[{Disk[d1/.β, .01]}]}, DisplayFunction→$DisplayFunction, AspectRatio→Automatic] ;

{1.11022*10^-15, {→1.69237, →3.1649}}

[Graphics:../HTMLFiles/index_430.gif]

Another try:

d1 = disc[{1.1, 1.15}] ;

d2 = disc[{0.9, 0.6}] ;

pγ = ParametricPlot[Evaluate[#1], {, 0, 2 π}, DisplayFunction→Identity] &/@{d1, d2} ;

dist = With[{v = (d1 - (d2/.→))}, (v . v)^(1/2)] ;

Plot3D[dist, {, 0, 2π}, {, 0, 2π}, PlotPoints→ {30, 30}] ;

[Graphics:../HTMLFiles/index_436.gif]

{z, β} = FindMinimum[dist, {, π, 0, 2π}, {, π, 0, 2π}]

Show[{pγ, Graphics[{Disk[d1/.β, .01]}]}, DisplayFunction→$DisplayFunction, AspectRatio→Automatic] ;

{7.1089*10^-16, {→3.63837, →1.46722}}

[Graphics:../HTMLFiles/index_441.gif]

Since, we are on a torus, we should exploit the symmetry... to be continued.

Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!