Geometric torus with signature 1,1

We proceed in a somewhat faster manner.

assume = {0<x_1<2π, 0<x_2<2π, 0<r<R} ;

f = {(R + r Cos[x_2]) Cos[x_1], (R + r Cos[x_2]) Sin[x_1], r Sin[x_2]} ;

pτ = ParametricPlot3D[Evaluate[f/.(inst = {R→2, r→1})], {x_1, 0, 2 π - 1.5}, {x_2, 0, 2π - 1}] ;

[Graphics:../HTMLFiles/index_362.gif]

J = Μd[f, 1, 2] ; J//MF

ShowMat[{ℊ = ΜPullback[f, 2, Id[3]] . ({{-1, 0}, {0, 1}}), T[J] . Id[3] . J, Τα[Id[3], 0, J]}//S]

( {{-(R + r Cos[x_2]) Sin[x_1], -r Cos[x_1] Sin[x_2]}, {Cos[x_1] (R + r Cos[x_2]), -r Sin[x_1] Sin[x_2]}, {0, r Cos[x_2]}} )

{( {{-(R + r Cos[x_2])^2, 0}, {0, r^2}} ), ( {{(R + r Cos[x_2])^2, 0}, {0, r^2}} ), ( {{(R + r Cos[x_2])^2, 0}, {0, r^2}} )}

the next plot shows the scalar curvature

ShowΜ[ℊ]

Plot3D[Evaluate[ΜS[ℊ]/.{R→2}], {x_2, 0, 2 π}, {r, 0.1, 1.9}] ;

metric ( {{-(R + r Cos[x_2])^2, 0}, {0, r^2}} )

christ {( {{0, -(r Sin[x_2])/(R + r Cos[x_2])}, {-(r Sin[x_2])/(R + r Cos[x_2]), 0}} ), ( {{-((R + r Cos[x_2]) Sin[x_2])/r, 0}, {0, 0}} )}

riemann↓

{1, 2, ( {{0, (r Cos[x_2])/(R + r Cos[x_2])}, {(Cos[x_2] (R + r Cos[x_2]))/r, 0}} )}

ricci ( {{-(Cos[x_2] (R + r Cos[x_2]))/r, 0}, {0, (r Cos[x_2])/(R + r Cos[x_2])}} )

scalar (2 Cos[x_2])/(r (R + r Cos[x_2]))

[Graphics:../HTMLFiles/index_375.gif]

The metric is Einstein, since Ric=λ g for

Solve[E0[ΜRic[Μℛ[ℊ]] - λ ℊ], λ]

{{λ→Cos[x_2]/(r (R + r Cos[x_2]))}}

We are interested in geodesics on the torus.

x0 = {-1.5, .4} ;

eqs = E0[Χγ[ℊ], Χ0[0][x0], Χ0[1][{Cos[α], Sin[α]}]]/.inst

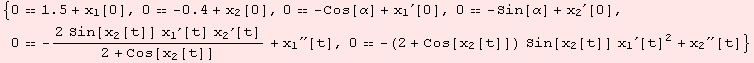
Done.

maxT = 10 ;

sol = Table[(NDSolve @@ {eqs, Χ[2], {t, -maxT 0, maxT}})[[1]], {α, 0, π/2, .15}] ;

ParametricPlot[Evaluate[Χ[2]/.sol], {t, -maxT 0, maxT}] ;

Show[pτ, ParametricPlot3D[Evaluate[{0, 0, .02} + f◦Χ[2]/.#1/.inst], {t, -maxT 0, maxT}, DisplayFunction→Identity] &/@sol] ;

[Graphics:../HTMLFiles/index_385.gif]

[Graphics:../HTMLFiles/index_386.gif]

Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!