index_11.html

Witch of Agnesi

Witch of Agnesi is a surface of revolution.

$γ = {2 a Tan[x_1], 2 a Cos[x_1]^2} ;$

$ParametricPlot[Evaluate[γ/.a→1], {x_1, -1.2, 1.2}] ;$

[Graphics:../HTMLFiles/index_294.gif]

$f = [γ[[1]], γ[[2]] {Cos[x_2], Sin[x_2]}]$

$p1 = ParametricPlot3D[Evaluate[.9 f/.a→1], {x_1, -1.2, 1.2}, {x_2, -3.5, 2}] ;$

${2 a Tan[x_1], 2 a Cos[x_1]^2 Cos[x_2], 2 a Cos[x_1]^2 Sin[x_2]}$

[Graphics:../HTMLFiles/index_298.gif]

The Euclidean space induces the following metric

$( {{-2 a^2 (-1 + Cos[4 x_1] - 2 Sec[x_1]^4), 0}, {0, 4 a^2 Cos[x_1]^4}} )$

The coefficient a, does not appear in the Riemann (1,3)-tensor field R.

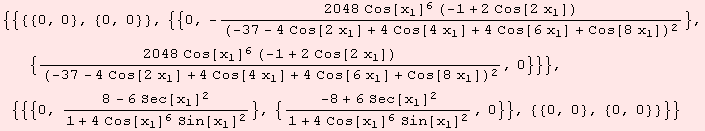
Geodesics on the witch of agnesi have the following intriguing property...

$sol = Χ★[x, 2]/.NDSolve[[ΧGeodesic[ℊ], {x_1[0] - .1, x_2[0] - .5}, {x_1^′[0] + 3., x_2^′[0] - .5}], Χ★[x, 2], {t, 0, T = 10}][[1]] ;$

[Graphics:../HTMLFiles/index_307.gif]

$sol = Χ★[x, 2]/.NDSolve[[ΧGeodesic[ℊ], {x_1[0] - .1, x_2[0] - .5}, {x_1^′[0] + 3., x_2^′[0] - 2.5}], Χ★[x, 2], {t, 0, T = 10}][[1]] ;$

[Graphics:../HTMLFiles/index_310.gif]

Created by Mathematica (December 22, 2006)