Laplace operator

Assume, we are on the sphere S^2 with metric

ℊS2p = ( {{r^2 Cos[x_2]^2, 0}, {0, r^2}} ) ;

φ is an eigenfunction to the Laplace operator on the sphere for any {v_1,v_2,v_3}∈^3\0.

φ = {r Cos[x_2] Sin[x_1], r Sin[x_2], r Cos[x_1] Cos[x_2]} . Τ★[v, 3]//S

r (Sin[x_2] v_2 + Cos[x_2] (Sin[x_1] v_1 + Cos[x_1] v_3))

The eigenvalue is

Μ△[ℊS2p, φ]/φ//S

-2/r^2

The same computation with respect to a different coordinate system is

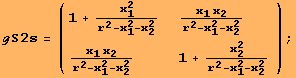
ℊS2s = ( {{1 + x_1^2/(r^2 - x_1^2 - x_2^2), (x_1 x_2)/(r^2 - x_1^2 - x_2^2)}, {(x_1 x_2)/(r^2 - x_1^2 - x_2^2), 1 + x_2^2/(r^2 - x_1^2 - x_2^2)}} ) ;

φ = {x_1, x_2, (r^2 - x_1^2 - x_2^2)^(1/2)} . Τ★[v, 3]//S

Μ△[ℊS2s, φ]/φ//S

v_1 x_1 + v_2 x_2 + v_3 (r^2 - x_1^2 - x_2^2)^(1/2)

-2/r^2

The code for the Laplacian is fairly simple:

? Μ△

Global`Μ△

Μ△[g_,f_]:=With[{df=Μd[f,ℓ[g]]},ΤC[Inv[g].(Μd[df,1]-df.ΜΓ[g])]]

In the next lines, we set up a parametrization f:S^3→^4 of the 3-sphere in ^4, compute the induced metric tensor, and check that φ:S^3→R defined below, is an eigenfunction of the Laplace operator.

MF[df = Μd[f = r ΜφSphere[3], 1, 3]]

MF[ℊS3p = T[df] . df//S]

Μ△[ℊS3p, φ = f . Τ★[v, 4]]/φ//S

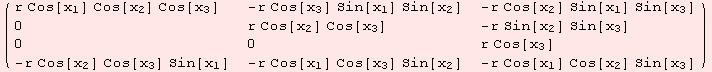
( {{r^2 Cos[x_2]^2 Cos[x_3]^2, 0, 0}, {0, r^2 Cos[x_3]^2, 0}, {0, 0, r^2}} )

-3/r^2

Now, back to the S^2. What is the explicit partial differential equation an eigenfunction function of the Laplace operator satisfies on S^2? We give the answer with respect to the two different coordinate systems introduced above.

Clear[f]

Μ△[ℊS2p, f[x_1, x_2]]//S

Μ△[ℊS2s, f[x_1, x_2]]//S

(-Tan[x_2] f^(0, 1)[x_1, x_2] + f^(0, 2)[x_1, x_2] + Sec[x_2]^2 f^(2, 0)[x_1, x_2])/r^2

1/r^2 (r^2 f^(0, 2)[x_1, x_2] - x_2^2 f^(0, 2)[x_1, x_2] - 2 x_1 f^(1, 0)[x_1, x_2] - 2 x_2 (f^(0, 1)[x_1, x_2] + x_1 f^(1, 1)[x_1, x_2]) + (r^2 - x_1^2) f^(2, 0)[x_1, x_2])

Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!