Change of basis

Recall: vectors are (1,0) tensors, covectors are (0,1) tensors, bilinear forms, such as scalar products, are (0,2) tensors. The determinant function of n vectors over ^n, equivalently a n×n matrix, is a (0,n) tensor. Matrices are (1,1) tensors. The commutator table of a Lie algebra is denoted by ad, which is a (1,2) tensor. The Riemannian curvature is a (1,3)-tensor, which is metrical equivalent to a (0,4)-tensor.

How can we stress the importance of the function Τα, which basis transform a (r,s)-tensor X with respect to the basis-transformation α. Note, α is the matrix that encodes the change of basis, equivalently α is vector space isomorphism. So how can we stress the importance? Lets show the impressive implementation :-)

? Τα

Global`Τα

Τα[X_,r_Integer,α_]:=S[Fold[T[#1,RotateRight[Range[r[X]],1]].#2&,X,Join@@{Table[T[Inv[α]],{r}],Table[α,{r[X]-r}]}]]

The input is tensor X, with contravariant rank r, and basis tranformation α. For example let

α = ({{1, 1}, {0, 1}}) ;

We transorm a vector, and a covector by α.

Τα[{a_1, a_2}, 0, α]

Τα[{a_1, a_2}, 1, α]

{a_1, a_1 + a_2}

{a_1 - a_2, a_2}

For a matrix, we have

Τα[({{a, b}, {0, c}}), 1, α]//MF

( {{a, a + b - c}, {0, c}} )

For instance in the chapter on Lie algebras, the function Τα is used to transform a given commutator tensor with respect to a change of vector space basis. Furthermore, Τα is the universal tool to extend tensors to left-invariant tensor fields. Briefly: Τα is omnipresent! Another application of Τα is computing the bundle metric. Lets make an easy illustration. Consider the following scalar product defined by

MF[ℊ = Τ★[g, 3]/.{g_3, g_5} →0]

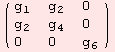
( {{g_1, g_2, 0}, {g_2, g_4, 0}, {0, 0, g_6}} )

Usually, for two vectors U,V, we use notation such as g.U.V of V.g.U in order to compute the scalar-product.

U = Τ★[u, 3]

V = Τ★[v, 3]

ℊ . U . V

U . ℊ . V

{u_1, u_2, u_3}

{v_1, v_2, v_3}

(g_1 u_1 + g_2 u_2) v_1 + (g_2 u_1 + g_4 u_2) v_2 + g_6 u_3 v_3

(g_1 u_1 + g_2 u_2) v_1 + (g_2 u_1 + g_4 u_2) v_2 + g_6 u_3 v_3

A more complicated, but more general formula involves Τα and the information that U,V are (1,0)-tensors.

Total[Τα[U, 1, Inv[ℊ]] V, 1]

(g_1 u_1 + g_2 u_2) v_1 + (g_2 u_1 + g_4 u_2) v_2 + g_6 u_3 v_3

For matrices there is the well known scalar product A:B (by notation with respect to g=Id), which yields

Total[(A = Τ★[a, {3, 3}]) (B = Τ★[b, {3, 3}]), 2]

Since a matrix is a (1,1)-tensor, we have the equivalent computation by,

Total[Τα[A, 1, Inv[Id[3]]] B, 2]

However, with respect to our special scalar product g as defined above, we would write

Total[Τα[A, 1, Inv[ℊ]] B, 2]//S

The formula is called bundle metric, which is implemented by the command Μg

? Μℊ

Global`Μg

Μg[g_,X_,Y_,r_Integer:1]:=Total[Τα[X,r,Inv[g]] Y,r[X]]

Application is evident from the discussion above:

Μℊ[ℊ, U, V]

Μℊ[ℊ, A, B, 1]//S

(g_1 u_1 + g_2 u_2) v_1 + (g_2 u_1 + g_4 u_2) v_2 + g_6 u_3 v_3

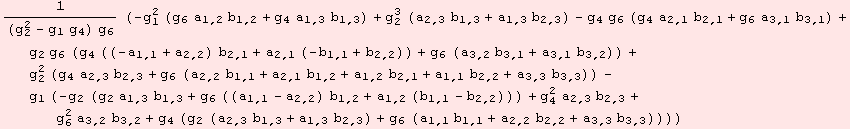
The bundle metric easily extends to a norm on the space of (r,s)-tensors.

? ΜNorm

Global`ΜNorm

ΜNorm[ℊ_, X_, r_Integer : 1] := Abs[Μℊ[ℊ, X, X, r]]^(1/2)
Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!