Symmetrizing, alternating, wedging

A square matrix decomposes into symmetric and skew-symmetric part. ΤS and ΤA perform these linear projections.

X = Array[2 Random[Integer, {-2, 2}] &, {4, 4}] ; X//MF

TF[{{"symmetric", "skew symmetric", "original"}, ShowMat[{Τ[X], Τ[X], Τ[X] + Τ[X]}]}]

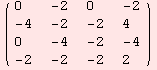
( {{0, -2, 0, -2}, {-4, -2, -2, 4}, {0, -4, -2, -4}, {-2, -2, -2, 2}} )

symmetric skew symmetric original
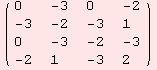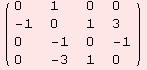( {{0, -3, 0, -2}, {-3, -2, -3, 1}, {0, -3, -2, -3}, {-2, 1, -3, 2}} ) ( {{0, 1, 0, 0}, {-1, 0, 1, 3}, {0, -1, 0, -1}, {0, -3, 1, 0}} ) ( {{0, -2, 0, -2}, {-4, -2, -2, 4}, {0, -4, -2, -4}, {-2, -2, -2, 2}} )

The functions ΤS and ΤA that symmetrize and alternate work for tensors of arbitrary rank but with fixed dimension. For instance, consider the (0,4)-tensor X below. Due to its length, we do not show X, but we indicate that S(A(X))=A(S(X))=0.

X = Τ★[a, {4, 4, 4, 4}] ;

ShowMat[Τ[Τ[X]]]

ShowMat[Τ[Τ[X]]]

{zero…4×4×4, zero…4×4×4, zero…4×4×4, zero…4×4×4}

{zero…4×4×4, zero…4×4×4, zero…4×4×4, zero…4×4×4}

DGkernel encodes wedging of two tensors as

X_List∧Y_List := ([X] + [Y]) !/([X] ! [Y] !) Τ[X⊗Y] ;

r_∧X_ := r X ;

When wedging multiple tensors, use brackets. Have a look at the following simple example.

{2, 3, 4} ∧ {a, b, c}//MF

{x, y, z} ∧ ({2, 3, 4} ∧ {a, b, c})//S//ShowMat

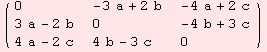
( {{0, -3 a + 2 b, -4 a + 2 c}, {3 a - 2 b, 0, -4 b + 3 c}, {4 a - 2 c, 4 b - 3 c, 0}} )

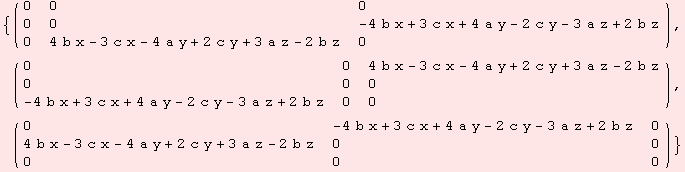
The following line of code sets up the tri/multi-linear-form that represents the determinant of 3×3 matrices.

ShowMat[myDet = Fold[#2∧#1&, 1, Id[3]]]

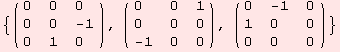
{( {{0, 0, 0}, {0, 0, -1}, {0, 1, 0}} ), ( {{0, 0, 1}, {0, 0, 0}, {-1, 0, 0}} ), ( {{0, -1, 0}, {1, 0, 0}, {0, 0, 0}} )}

Lets go two ways to obtain the determinant of the matrix X below.

MF[X = Τ★[a, {3, 3}]]

Det[X]

myDet . X[[1]] . X[[2]] . X[[3]]//Expand

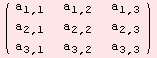
( {{a_ (1, 1), a_ (1, 2), a_ (1, 3)}, {a_ (2, 1), a_ (2, 2), a_ (2, 3)}, {a_ (3, 1), a_ (3, 2), a_ (3, 3)}} )

-a_ (1, 3) a_ (2, 2) a_ (3, 1) + a_ (1, 2) a_ (2, 3) a_ (3, 1) + a_ (1, 3) a_ (2, 1) a_ (3, 2) - a_ (1, 1) a_ (2, 3) a_ (3, 2) - a_ (1, 2) a_ (2, 1) a_ (3, 3) + a_ (1, 1) a_ (2, 2) a_ (3, 3)

-a_ (1, 3) a_ (2, 2) a_ (3, 1) + a_ (1, 2) a_ (2, 3) a_ (3, 1) + a_ (1, 3) a_ (2, 1) a_ (3, 2) - a_ (1, 1) a_ (2, 3) a_ (3, 2) - a_ (1, 2) a_ (2, 1) a_ (3, 3) + a_ (1, 1) a_ (2, 2) a_ (3, 3)

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!