Contraction

Contraction is one of the most important operations in tensor analysis. Lets illustrate the operations using the two tensors A,Y below.

MF[A = Τ★[a, {3, 3}]]

Y = {x_1, x_2, x_3}

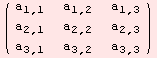
( {{a_ (1, 1), a_ (1, 2), a_ (1, 3)}, {a_ (2, 1), a_ (2, 2), a_ (2, 3)}, {a_ (3, 1), a_ (3, 2), a_ (3, 3)}} )

{x_1, x_2, x_3}

The matrix-vector product can be interpreted as an outer product followed by 2,3-contraction. The command for contraction is ΤC.

A . Y//MF

Dims[A⊗Y]

ΤC[A⊗Y, 2, 3]//MF

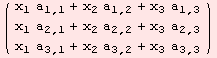
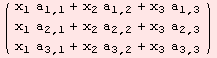
( {{x_1 a_ (1, 1) + x_2 a_ (1, 2) + x_3 a_ (1, 3)}, {x_1 a_ (2, 1) + x_2 a_ (2, 2) + x_3 a_ (2, 3)}, {x_1 a_ (3, 1) + x_2 a_ (3, 2) + x_3 a_ (3, 3)}} )

{3, 3, 3}

( {{x_1 a_ (1, 1) + x_2 a_ (1, 2) + x_3 a_ (1, 3)}, {x_1 a_ (2, 1) + x_2 a_ (2, 2) + x_3 a_ (2, 3)}, {x_1 a_ (3, 1) + x_2 a_ (3, 2) + x_3 a_ (3, 3)}} )

Lets move to a more complicated example. Consider the tensor X below.

X = Τ★[a, {2, 3, 4, 3, 1}] ;

Dims[X]

{2, 3, 4, 3, 1}

The only contraction we can perform on X is on dimensions 2 and 4, refered to 2,4-contraction. Have a look at the indicees, to understand how the computation is done. The remaining dimensions of the contracted tensor are 2,4,1.

ΤC[X, 2, 4]

Dims[%]

{2, 4, 1}

We get an error for any other combination such as

ΤC[X, 2, 3]

ΤC :: dimensions : conflict

The 1,2-contraction of a square matrix X is simply the trace of the matrix X:

X = Τ★[a, {3, 3}] ; X//MF

ΤC[X, 1, 2]

Tr[X]

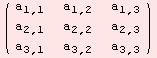
( {{a_ (1, 1), a_ (1, 2), a_ (1, 3)}, {a_ (2, 1), a_ (2, 2), a_ (2, 3)}, {a_ (3, 1), a_ (3, 2), a_ (3, 3)}} )

a_ (1, 1) + a_ (2, 2) + a_ (3, 3)

a_ (1, 1) + a_ (2, 2) + a_ (3, 3)

If the dimensions to be contracted on are not specified, then 1,2-contraction is performed.

ΤC[X]

a_ (1, 1) + a_ (2, 2) + a_ (3, 3)

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!