Outer sums and products

To combine tensors in an outer sum, they have to be of the same rank. Thus we may combine

{a, b} ⊕ {1, 2, 3}

({{a, b}, {c, d}}) ⊕Τ★[e, {3, 3}]//MF

{a, b, 1, 2, 3}

( {{a, b, 0, 0, 0}, {c, d, 0, 0, 0}, {0, 0, e_ (1, 1), e_ (1, 2), e_ (1, 3)}, {0, 0, e_ (2, 1), e_ (2, 2), e_ (2, 3)}, {0, 0, e_ (3, 1), e_ (3, 2), e_ (3, 3)}} )

We may also take the outer sum of two ad tensors that define Lie algebras.

ShowAd[ad★[a, 2]]

ShowAd[ad★[a, 2] ⊕ad★[b, 1]]

( {{0, e_1 a_ (1, 2, 1) + e_2 a_ (2, 2, 1)}, {-e_1 a_ (1, 2, 1) - e_2 a_ (2, 2, 1), 0}} )

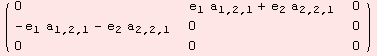
( {{0, e_1 a_ (1, 2, 1) + e_2 a_ (2, 2, 1), 0}, {-e_1 a_ (1, 2, 1) - e_2 a_ (2, 2, 1), 0, 0}, {0, 0, 0}} )

Tensors of any rank are eligible to be combined in an outer product. Examples are given below.

{a, b} ⊗ {1, 2, 3}//MF

ShowMat[myp = {a, b} ⊗ ({{, 2}, {3, 4}, {5, 6}})]

Dims[myp]

( {{a, 2 a, 3 a}, {b, 2 b, 3 b}} )

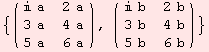
{( {{ a, 2 a}, {3 a, 4 a}, {5 a, 6 a}} ), ( {{ b, 2 b}, {3 b, 4 b}, {5 b, 6 b}} )}

{2, 3, 2}

As a matter of definition - and in fact recursion - the tensor product between a factor x∈R an a tensor X simply is the multiple x of the tensor.

x⊗Τ★[e, {3, 2}]

Τ★[e, {2, 3}] ⊗77

{{x e_ (1, 1), x e_ (1, 2)}, {x e_ (2, 1), x e_ (2, 2)}, {x e_ (3, 1), x e_ (3, 2)}}

{{77 e_ (1, 1), 77 e_ (1, 2), 77 e_ (1, 3)}, {77 e_ (2, 1), 77 e_ (2, 2), 77 e_ (2, 3)}}

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!