Default constructors

Default constructors help you to quickly instanciate the objects you would like to do math with. An example: Τ★ creates tensors of arbitrary rank.

{Τ★[A, {3, 3}], Τ★[b, {3}], Τ★[A, {3, 3}] . Τ★[b, {3}]}//ShowMat

As we demonstrate above, Τ★ is used to obtain general expression for formulas in linear algebra. Functions of the DGkernel acting as default constructors, usually have a 5-star ★ attached in the command name. Τ★ instanciates tensors of arbitrary tensor rank.

Τ★[A, {2, 3, 4}]

%//Dims

{2, 3, 4}

To set up an symmetric (0,2)-tensor with symbolic entries, we use ΤS★. For skew-symmetric matrices, please use ΤA★.

{Τ★[g, 4], Τ★[g, 4]}//ShowMat

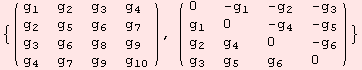
{( {{g_1, g_2, g_3, g_4}, {g_2, g_5, g_6, g_7}, {g_3, g_6, g_8, g_9}, {g_4, g_7, g_9, g_10}} ), ( {{0, -g_1, -g_2, -g_3}, {g_1, 0, -g_4, -g_5}, {g_2, g_4, 0, -g_6}, {g_3, g_5, g_6, 0}} )}

The Riemannian curvature (1,3)-tensor field R of a semi-Riemannian manifold becomes a (1,3)-tensor when restricted to the tangent space of a point x. The tensor ℛ_x has special symmetries. Some of them are allready encoded in the command

Showℛ[ℛx = Τℛ★[r, 3]]

ℓ[Vars[ℛx]]

ℛ_ (1, 2, j)^i ℛ_ (1, 3, j)^i ℛ_ (2, 3, j)^i
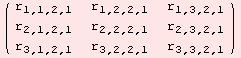( {{r_ (1, 1, 2, 1), r_ (1, 2, 2, 1), r_ (1, 3, 2, 1)}, {r_ (2, 1, 2, 1), r_ (2, 2, 2, 1), r_ (2, 3, 2, 1)}, {r_ (3, 1, 2, 1), r_ (3, 2, 2, 1), r_ (3, 3, 2, 1)}} ) ( {{r_ (1, 1, 3, 1), r_ (1, 2, 3, 1), r_ (1, 3, 3, 1)}, {r_ (2, 1, 3, 1), r_ (2, 2, 3, 1), r_ (2, 3, 3, 1)}, {r_ (3, 1, 3, 1), r_ (3, 2, 3, 1), r_ (3, 3, 3, 1)}} )

24

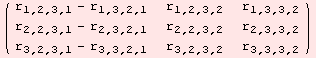Instead of 3·3·3=27 variable, R★ comes with 24. If we input the scalar-product, which originates from the metric at the point x, we get the exact number of degrees of freedom, namely 6.

Showℛ[ℛx = Τℛ★[r, ({{0, 0, 1}, {0, 1, 0}, {1, 0, 0}})]]

ℛx

ℓ[Vars[ℛx]]

ℛ_ (1, 2, j)^i ℛ_ (1, 3, j)^i ℛ_ (2, 3, j)^i
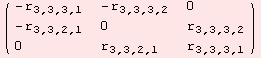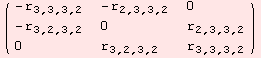( {{-r_ (3, 3, 2, 1), -r_ (3, 2, 3, 2), 0}, {-r_ (3, 2, 2, 1), 0, r_ (3, 2, 3, 2)}, {0, r_ (3, 2, 2, 1), r_ (3, 3, 2, 1)}} ) ( {{-r_ (3, 3, 3, 1), -r_ (3, 3, 3, 2), 0}, {-r_ (3, 3, 2, 1), 0, r_ (3, 3, 3, 2)}, {0, r_ (3, 3, 2, 1), r_ (3, 3, 3, 1)}} ) ( {{-r_ (3, 3, 3, 2), -r_ (2, 3, 3, 2), 0}, {-r_ (3, 2, 3, 2), 0, r_ (2, 3, 3, 2)}, {0, r_ (3, 2, 3, 2), r_ (3, 3, 3, 2)}} )

6

Another useful constructor, produces a starting point for a commutator (1,2)-tensor of a Lie algebra.

ad = ad★[a, 3]

ShowAd[ad]

not jacobian.

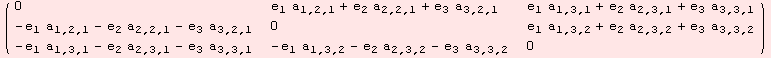
However, as informed by the command ShowAd, the tensor does not (yet) satisfy the Jacobi identity. The Jacobi identity reduces to non-linear equations, so the set of all valid Lie algebra commutator tensors is not a vector space.

Created by Mathematica  (September 30, 2006) Valid XHTML 1.1!