Autonomous Go-Kart

The go-kart is a mobile robot that has been in operation at the Innovationpark in Dübendorf/Switzerland since December 2017. The go-kart is a project by the Frazzoli group at the IDSC of ETH Zürich.

Between January 2017 and December 2019 I was a member of the group and in charge of the software architecture of the go-kart project. During my time at ETH, we achieved the following milestones:

Autonomous driving started as pure pursuit of a predefined track on day four.
The first demonstration of autonomous driving to the general public was conducted three months into the project.
Motion planning around changing obstacles was implemented after six months.
Autonomous lap racing faster than human driving was achieved 16 months into operation.

In September 2019, the go-kart project was relocated to the Rieter area in Winterthur/Switzerland.

Until December 2019, the project was coordinated by the following ETH staff: Mechanics by Daniel Wagner. Electronics by Marc-Andre Corzillius, and Marcus Aaltonen. Software architecture and review of student contributions by Jan Hakenberg. Supervision of student projects by Jan Hakenberg, Jacopo Tani, Andrea Censi, and Alessandro Zanardi.

Thesis Projects

The following students have contributed to the development during their thesis projects at the Frazzoli group at the Institute for Dynamic Systems and Control of the ETH Zürich. Thank you!

Noah Isaak	Drive-by-wire Conversion of a Go-kart
Richard von Moos	Drive-by-wire Conversion of a Go-kart
Jonas Londschien	An Anytime Generalized Label Correcting Method for Motion Planning
Yannik Nager	What lies in the shadows? Safe and computation-aware motion planning for autonomous vehicles using intent-aware dynamic shadow regions
Mario Gini	Event-Based Vision Control of Autonomous Vehicles
Valentina Cavinato	Lidar perception for autonomous vehicles
Christian Fluri	Learning to Operate a Fleet of Cars
Marc Heim	Model Predictive Contouring Control of an Autonomous Go-kart
André Stoll	Multi-Objective Optimization Using Preference Structures
Oliver Brinkmann	Averaging on Lie Groups: Applications of Geodesic Averages and Biinvariant Means
Michael von Büren	Data-Driven Vehicle Dynamics Modeling for an Autonomous Go-Kart
Joel Gächter	Subdivision-Based Clothoids in Autonomous Driving
Antonia Mosberger	Advanced Driver Assistance Systems on a Go-Kart

Learn as much mathematics as you can, particularly applied math.
The areas of mathematics we use most heavily today are Euclidean and affine
geometry, trigonometry, linear algebra, calculus and numerical analysis.
We don't really know what the mathematical tools of tomorrow might be,
so we're counting on the next generation of employees to tell us.
Tony DeRose

Video Recordings

The videos below show selected functionality.

Not all those who wander are lost.
Tolkien

Software Architecture

visualization of sensor and control data

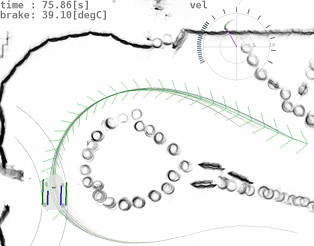
The software architecture has the following non-standard characteristics:

computation with quantities, i.e. numbers with physical units,
class introspection for parameter management,
restriction to only one lcm-message type,
few processes with multi-threading in favor over numerous processes.

The choice of tools permits development on all major operating systems, and results in an amortized compile time of below 1[s].

The source code comprises of 110k lines of code from over 5000 source files that contribute to the operation of the go-kart. The functionality is distributed over six libraries, which are ordered from general to specific:

tensor is a library for linear algebra and tensor computations. The implementation defines a tensor recursively as either a list of tensors, or a scalar. Scalar encoding is in exact or numeric precision. All algorithms support the use of quantities. Features include probability distributions for random variate generation, kernel functions, and spectral analysis. The API is inspired by Wolfram's Mathematica.

sophus is a library for computational geometry on manifolds and Lie-groups. Functionality includes the smoothing of sequences of noisy measurements, the generation of smooth curves from control points, and the interpolation of data from non-linear spaces. Geodesic averages and biinvariant means substitute affine combinations in traditional algorithms for linear data. The non-linear operations are relevant for car-like mobile robots, and drones.

subare implements the iterative methods that are detailed in the book on reinforcement learning by Sutton and Barto. Algorithms include action-value iteration, q-learning, true-online sarsa, prioritized sweeping, monte carlo with exploring starts, etc. The methods have contributed to the development of simple control strategies for robots in simulation.

owl is a library for motion planning, simulation, and visualization. The two planning methods, generalized labeling correction, and rapidly exploring random trees, as well as a collection of state space models, obstacle regions, cost functions, and spherical and conic goal regions with efficient heuristics are readily available. Shadow regions, and preference structures for multi-objective optimization have been incorporated as novel concepts in motion planning.

retina reads out various sensing devices including lidars, event-based cameras, inertial measurement units, and GPS. Data processing as part of the perception pipeline are visual features tracking, event-based simultaneous localization and mapping, and clustering of lidar points.

gokart contains interfaces to the actuators of the go-kart, lidar-based localization and state estimation, modules for hardware preservation and safety embedded in the hierarchical driving logic. Power steering, and anti-lock braking facilitate manual driving. Obstacle mapping, and track boundary parameterization are used in motion planning. The autonomous modes are pure pursuit, clothoid pursuit, and model predictive contouring control.

The repositories can be downloaded from idsc-frazzoli/github.

Example is not the main thing in influencing others.
It is the only thing.
Albert Schweitzer